Реферат: Решение задачи об оптимальной интерполяции с помощью дискретного преобразования Фурье (ДПФ)

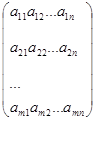(8)

называется матрицей.

Коротко матрицу обозначают так: , ;

где - элемент данной матрицы, который находится в i-й строке и j-м столбце матрицы А.

5

Некоторые свойства матриц:

1. сумма С = А + В двух матриц А и В одного размера mn – это матрица

С = (с), где с = a + b для всех i, j;

сумма матриц разных размеров не определяется.

2.Произведение С = λА матрицы А и элемента λС – это матрица того же размера, что и А, причём при всех i, j.

3.Произведение С = АВ матрицы А размера mn и матрицы В размера np – это матрица С размера mp такая, что

Произведение матриц в общем случае некоммутативно, т.е АВ≠ВА.

Транспонированная матрица (по отношению к матрице А) – такая матрица, что .

Совокупность элементов квадратной матрицы называется главной диагональю матрицы.

Матрица, у которой элементы, стоящие на главной диагонали, равны единице, а все остальные элементы равны 0, называется единичной матрицей и обозначается буквой Е.

Напомним, что

АЕ = А и ЕА = А.

Матрица называется ортогональной, если строки образуют ортогональную систему векторов и норма каждой строки равна единице.

Квадратная матрица называется симметрической, если

.

6.Определители. Всякое расположение чисел 1, 2, …, n в некотором определённом порядке называется перестановкой из n чисел.

Говорят, что в данной перестановке числа i и j составляют инверсию, если i>j, но i стоит в этой перестановке раньше j.

Перестановку называют чётной, если её символы составляют чётное число инверсий, и нечётной – в противоположном случае.

Всякое взаимно однозначное отображение А множества первых n натуральных чисел на себя называется подстановкой n-й степени, причём, очевидно, всякая подстановка А может быть записана при помощи двух перестановок, подписанных одна под другой.

6

Подстановка А будет чётной, если общее число инверсий в двух строках любой её записи чётно, и нечётной – в противоположном случае.

Определителем n-го порядка называется алгебраическая сумма n! членов, составленная следующим образом: членами служат всевозможные произведения n элементов матрицы, взятых по одному в каждой строке и в каждом столбце, причём член берётся со знаком плюс, если его индексы составляют чётную подстановку и со знаком минус в противоположном случае.

Для определителя квадратной матрицы А используется обозначение |A| или detA.