Реферат: Теория случайных чисел
3. Бернуллиевая случайная величина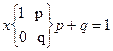 
4. Равномерное распределение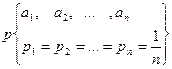 
Непрерывные случайные величины (НСВ).
1. Равномерное распределение
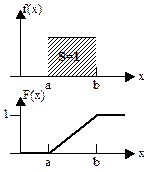
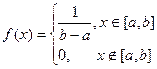
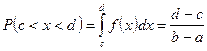
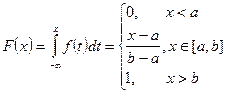
2. Треугольное распределение Симпсона
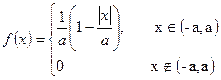
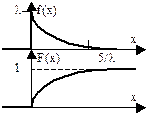3. Экспоненциальное (показательное) распределение. Имеет важное значение в теории массового обслуживания и теории надежности.
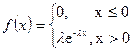
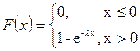
l - интенсивность.
3. Нормальный закон распределения.
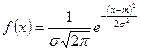, s>0
s=1, m=0 – нормальное стандартное распределение (m-мат. ожидание)
- такой подстановкой любое нормальное распределение приводится к стандартному.
При фиксированном s и изменяющемся m, кривая двигается вдоль Ох, не изменяя формы.
При фиксированном m и изменяющемся s (s1 <s2 <s3 ), кривая вытягивается вдоль оси ординат, но площадь фигуры под каждой кривой = 1.
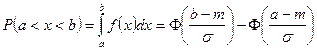
Функция Лапласа: 
Операции со случайными величинами
Со случайными величинами, рассмотренными на одном и том же интервале исходов опыта, можно обращаться как с обычными числами и функциями.
X:
| X | a1 | a2 | … | an |
| p | p1 | p2 | … | pn |
Y=j(x)
Нужно найти закон распределения СВ Y. yk =j(ak ), где k=1,2,…,n.
P(y=yk )=P(x=ak )=Pk
Если все значения СВ Y различны, то их надо проранжировать и указать соответствующие вероятности.
Если СВ Y принимает совпадающие значения, то их надо объединить под общей вероятностью, равной сумме соответствующих вероятностей, а после в ранжированном виде привести в таблице.
X={0,1,2,…,9}, P(x=k)=0.1, k=0,1,…,9, Y=x2 , Z=(x-5)2 .
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| P | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Y | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| Py | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Z | 25 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
| Pz | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
Закон распределения СВ Z:
| Z | 0 | 1 | 4 | 9 | 16 | 25 |
| Pz | 0.1 | 0.2 | 0.2 | 0.2 | 0.2 | 0.1 |