Реферат: Теория случайных чисел
3. По известным двумерным находятся соответствующие одномерные
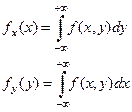
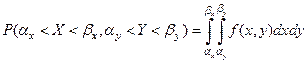
В случае статистической независимости СВ Х и У
F(x,y)=Fx (x)×Fy (y)
f(x,y)=fx (x)×fy (y)
F(x,y)=Fx (x)×Fy (y/x)=Fx (x/y) – для условных
f(x,y)=fx (x) ×f(y/x)=fy (y) ×f(x/y)
Раздел 4. Числовые характеристики СВ
Исчерпывающие представления о СВ дает закон её распределения.
Во многих задачах, особенно на заключительной стадии, возникает необходимость получить о величине некоторое суммарное представление: центры группирования СВ – среднее значение или математическое ожидание, разброс СВ относительно её центра группирования.
Эти числовые характеристики в сжатой форме отражают существенные особенности изучаемого распределения.
Математическое ожидание (МО)
М(х), МО(х), mx , m
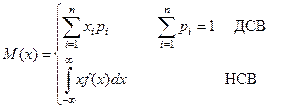
Основные свойства МО:
1. М(х) СВ Х Þ Хmin £М(х)£Хmax
2. М(С)=С МО постоянной величины есть величина постоянная
3. М(Х±У)=М(Х) ±М(У)
4. М(Х×У)=М(х) ×М(у) Þ М(Сх)=СМ(х) – МО произведения двух независимых СВ
5. М(аХ+вУ)=аМ(Х)+вМ(У)
6. М(Х-m)=0 – МО СВ Х от её МО.
МО основных СВ
Дискретные Случайные Величины
1. Биноминальные СВ МО(Х)=np
2. Пуассоновские СВ МО(Х)=l
3. Бернуллиевы СВ МО(Х)=р
4. Равномерно распред. СВ ![]()
Непрерывные Случайные Величины
1. Равномерно распределенная СВ ![]()
2. Нормально распределенная СВ MO(X)=m
3. Экспоненциально распределенная СВ ![]()