Реферат: Теория случайных чисел

СВ X,Y заданы в 1 опыте.

Исход опыта	E1	E2	…	En
Вероятность исхода	P1	P2	…	Pn
X	X1	X2	…	Xn
Y	Y1	Y2	…	Yn
Z= j (XY)	Z1	Z2	…	Zn

Сложнее, если СВ задана только своим распределением:

X	a1	a2	…	an
Р	p1	p2	…	pn

Y	b1	b2	…	bn
Р	g1	g2	…	Gn

Z=X+Y

СВ Z принимаетзначения a_k +b_s , где a_k =a₁ ,a₂ ,…,a_n ; b_s =b₁ ,b₂ ,…b_m .

Общее количество возможных значений СВ = m×n.

P(Z=a_k +b_s )=P(X=a_k , Y=b_s )

Для нахождения такой вероятности необходимо знать закон совместного распределения СВ X и Y.

Набор точек (a_k ,b_s ) вместе с вероятностями P(X=a_k , Y=b_s ) называется совместным распределением СВ X и Y . Обычно такое распределение задается таблицей.

Определение закона распределения суммы СВ по законам распределения слагаемых называется композицией законов распределения .

X \Y	b1	b12	…	bs	…	bm	Px
a1	P11	P12	…	P1s	…	P1m	P1
a2	P21	P22	…	P2s	…	P2m	P2
…	…	…	…	…	…	…	…
ak	Pk1	…	…	Pks	…	Pkm	Pk
…	…	…	…	…	…	…	…
an	Pn1	Pn2	…	Pns	…	Pnm	Pn
Py	g1	g2	…	gs	…	gm	1

Наиболее просто вероятности P_ks находятся в случае независимости СВ X и Y. Две СВ X и Y называются независимыми тогда и только тогда, когда

P(X=a_k , Y=b_s )=P(X=a_k )×P(Y=b_s )

P_ks =P_k ×P_s

По известному закону распределения совместного распределения СВ X и Y могут быть найдены одномерные законы распределения СВ X и Y.

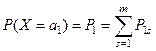
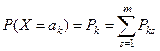
Теорема . Если СВ Х,Y являются независимыми, то любые функции j(Х) и y(У) от этих величин также являются независимыми.

Распределение функции от случайной величины

Х – непрерывная СВ

. По закону распределения СВ Х. Найти закон распределения СВ Y.

Если СВ ХÎ[х₀ ,х₁ ], то Î [y₀ ,y₁ ].

Предполагается, что функция j(х) является однозначной и имеет обратную функцию q(y).

Воспользовавшись элементами вероятности:

получим .

Закон распределения не меняется, если q(y) является линейной.

f_y (y)=f_x (x).

Многомерные законы распределения СВ

Часто при решении практических задач мы имеем дело не с одной, а с совокупностью нескольких случайных величин, которые взаимосвязаны .

nx₁ ,x₂ ,…,x_n n -мерная случайная величина – совокупность n взаимосвязанных случайных величин. Для ее описания используются многомерные законы распределения.

Двумерные функции распределения

X,YF(x,y)=P(X<x,Y<Y)

Функция F ( x , y ) обладает свойствами, аналогичными свойствам одномерной функции:

– не убывающая 1. x₂ ³x₁ ÞF(x₂ ,y)³F(x₁ ,y)

– не отрицательная y₂ ³y₁ ÞF(x,y₂ )³F(x,y₁ )

0£F(x,y)£ 1 2. F(¥,¥)= 1 F(-¥,-¥)=0

3. F_x (x)=P(X<x+=P(X<x,Y<¥)=F(x,¥)

F_y (y)=P(Y<y)=P(X<¥,Y<y)=F(¥,y)

f ( x , y ) – функция плотности вероятности совместного распределения величин x и y .

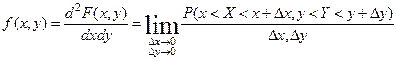
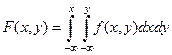
1. f(x,y)³0