Реферат: Теория случайных чисел

1. R=X_max -X_min – размах СВ

2. M(|X-m|) – среднее абсолютное отклонение СВ от центра группирования

3. M(X-m)² – дисперсия – МО квадрата отклонения СВ от центра группирования

M(X-m)² =D(X)=s² =s_x ² =s² (X)

– среднеквадратическое отклонение (стандартное отклонение).

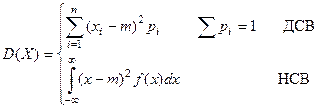
Основные свойства дисперсии:

1. Для любой СВ Х: D(X)³0. При Х=constD(X)º0.

2. D(X)=M(X² )-M² (X)=M(X² -2mX-m² )

3. D(cX)=c² D(X)

4. D(X+c)=D(X)

5. D(X+Y)=D(X)+D(Y), D(X-Y)=D(X)+D(Y)

В общем случае:

D(X+Y)=M(X+Y-m_{x + y} )² =M((X-m_x )+(Y-m_y ))² =M((X=m_x )² +2(X-m_x )(Y-m_y )+(Y-m_y )² )=

=D(X)+2M((X-m_x )(Y-m_y ))+D(Y). Второй член этого выражения называется корреляционным моментом . m_{x + y} =M(X)+M(Y)=m_x +m_y . D(X)=M(X-m_x )² .

M((X-m_x )(Y-m_y ))=K(X,Y)=K_xy =cov(x,y) – ковариация

K_xy /s_x s_y =r_xy – коэффициент корреляции

6. Независимые СВ: D(XY)=D(X)D(Y)+M² (X)D(Y)+M² (Y)D(X)

Дисперсия основных СВ

ДСВ

1. Биноминальные D(X)=npq

2. Пуассоновские D(X)=l

3. Бернуллиевы D(X)=pq

НСВ

1. Равномерно распределенные D(X)=(b-a)² /12

2. Нормально распределенные D(X)= s²

3. Экспоненциально распределенные D(X)=1/l²

Математическое ожидание и дисперсия суммы случайных величин

X₁ ,X₂ ,…,X_n – независимые СВ с одинаковым законом распределения.