Реферат: Теория вероятности

В то же время не совместны, тогда по теории сложения вероятностей .

Пример : Из каждых 10 посетителей магазина 6 не делают покупок.

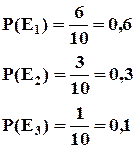Вероятность появления хотя бы одного из этих событий равна 1.

Два единовременно возможных события, образующих полную группу, называются противоположными (например: орел и решка).

Сумма вероятностей противоположных событий равна 1.

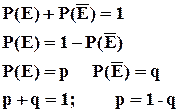
Если случайное событие Е имеет весьма малую вероятность, то практически можно считать, что в единичном испытании это событие не произойдет. Если .

На практике весьма малой считается вероятность Р(Е)£0,1.

Игнорировать возможность появления редких событий в виду их малой вероятности на практике можно только в том случае, если это событие не имеет катастрофических последствий.

Если случайное событие имеет вероятность весьма близкую к 1, то в конкретном испытании это событие, скорее всего, произойдет.

5. Теорема умножения вероятностей.

Два события считаются независимыми , если вероятность одного из них не зависит от появления или не появления другого события.

Независимые события имеют место при повторном отборе, когда отобранная в первом испытании единица после регистрации исхода испытания возвращается в генеральную совокупность.

Вероятность совместного появления двух независимых событий Е₁ и Е₂ равна произведению их вероятностей.

n(E₁ ) – число исходов благоприятных событию Е₁ ;

n(E₂ ) – число исходов благоприятных событию Е₂ ;

n₁ – число исходов благоприятных и неблагоприятных событию Е₁ ;

n₂ - число исходов благоприятных и неблагоприятных событию Е₂ .

Поскольку каждый конкретный результат испытания может осуществиться в комбинации с любым другим возможным результатом испытания, вероятность совместного появления событий Е₁ и Е₂ можно определить по формуле:

Несколько событий называются совместно независимыми или независимыми в совокупности, если каждая из них и любая комбинация из них содержащая либо все остальные события, либо часть из них – есть события независимые.

Е₁ Е₂ Е₃

Е₁ и Е₂ – независимы;

Е₁ и Е₃ – независимы;

Е₂ и Е₃ - независимы;

Е₁ и Е₂ Е₃ – независимы;