Реферат: Теория вероятности

Формула, которая определяет вероятность появления события Е k-раз в n-независимых испытаниях, называется формулой Бернулли . А схема отбора из дихотомной совокупности схемой Бернулли (или схемой возвращаемого шара или схемой повторного отбора).

Пример : Для обслуживания покупателей супермаркета в час пик без очередей должно работать не менее 6 контролеров-кассиров из 8. Вероятность отсутствия одного из работников составляет 0,1. Найти вероятность работы расчетно-кассового узла без очередей.

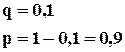
Поскольку нас устраивает работа 6, 7, 8 кассовых кабин, то вероятность появления одного из этих несовместных событий будет определяться по формуле сложения вероятностей. Каждая из этих вероятностей может определяться по формуле Бернулли.

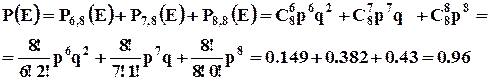
Таким образом, в 96 случаях из 100 очередей не будет.

Если при фиксированной численности n-повторного отбора из дихотомной совокупности изменять величину k, то полученное распределение вероятности будет называться биномиальным. Поскольку его ординаты представляют собой элементы разложения бинома .

Число наступления событий в n-независимых испытаниях называется наивероятнейшим , если этому числу соответствует наибольшая вероятность.

При этом если k смешанное число, то в результате выбирается ближайшее к этому смешанному числу, но меньше его, целое число.

В примере с кассирами .

Математическое ожидание М( k ) числа появления событий Е в n-независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.

Если перейти от абсолютного числа раз появления события к плотностям распределения вероятностей, то будет равно p.

Дисперсия биномиального распределения , - по плотности.

График биномиального распределения зависит от соотношения p и q. Если p равно q и равно 0,5, то распределение симметрично, в противном случае (p≠q) наблюдается асимметрия или скошенность полигона.

Показатель асимметрии биномиального распределения определяется по формуле:

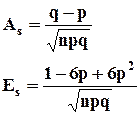
Если , то высота биномиального распределения соответствует высоте кривой нормального распределения. Доказано, что с увеличением числа испытаний значения , а биномиальное распределение стремится к нормальному распределению.

9. Вероятность редких событий. Формула Пуассона.

Применение формулы Бернулли сопряжено с расчетами трех факториалов, что при достаточно больших значениях n, k, n-q, осложняет задачу. Поэтому статистики математики разработали ряд примерных методов, заменяющих формулу Бернулли при решении некоторых частных и общих задач.

Пример : Определение вероятности появления редких событий , k-раз, в n независимых испытаниях. Причем подразумевается нефиксированное, а бесконечно большое количество испытаний ( ). При этом . Такая вероятность определяется по формуле Пуассона (альтернативные независимые события).

- математическое ожидание;

Формула Пуассона выводится из формулы Бернулли и после ряда преобразований выглядит следующим образом 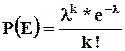, где k – количество раз, которое произойдет редкое событие.

Эта формула применяется в прикладных разработках, в теории массового обслуживания (теории очередей), которая используется для расчета оптимального числа точек обслуживания, числа бензоколонок, числа рабочих мест операционистов в банке (такое число, чтобы не было очередей).

Кроме того, формула Пуассона применяется в ситуациях, когда не требуется высокая точность расчетов, а вероятность события p не велика.