Реферат: Теория вероятности

В 1730 г. формула для приближения расчета значений для случая, когда p=q=0,5 предложил французский математик де Муавр.

Позднее в 1783 г. Лаплас обобщил результаты, полученные де Муавром, в своей теореме. Если вероятность p появления события Е в каждом испытании постоянна и отлична от 0 и 1, то вероятность появления события Е в n испытаниях равно k раз приближенно равна значению функции:

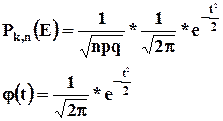
Созданы специальные таблицы значений функции в зависимости от величины t. t – стандартизированное значение.

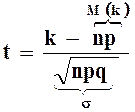
Пример : Найти вероятность того, что 80 из 1000 приобретут мужскую обувь, если вероятность покупки обуви p=0,11 (по данным из наблюдений за предыдущий период).

1)

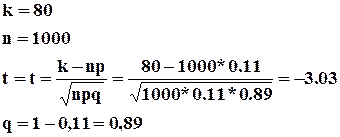
Поскольку в функции использована четная степень t – функция положительна, то есть .

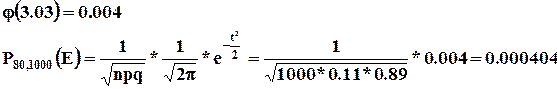
Таким образом, только в 404 случаях из 1 млн. ровно 80 из 1000 посетителей приобретут мужскую обувь.

2)

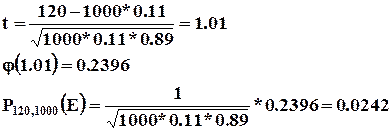
Таким образом, в 242 случаях из 10000 ровно 120 из 1000 посетителей приобретут мужскую обувь.

11. Интегральная формула Лапласа.

Локальная теорема Лапласа имеет важное значение, однако ее практическое значение ограничено. На практике важно знать вероятность того, что событие Е произойдет число раз, заданное в определенных пределах.

Пример : Вероятность приобретения покупателями мужской обуви от 80 до 120 человек из 1000.

, то есть, равна сумме вероятностей несовместных событий покупки 1000 посетителей конкретного числа пар обуви в пределах от 80 до 120 пар обуви.

Каждое из слагаемых определяется по локальной формуле Лапласа. Высокая трудоемкость задачи очевидна, поэтому рациональным способом решения задачи является интегрирование локальной функции Лапласа.

Если вероятность p появления событий Е в каждом испытании постоянна и отлична от 0 и 1 , то

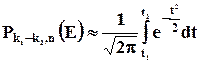, при этом

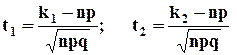
Интегрированная функция описывает распределение вероятности полной группы событий, поэтому ее общая площадь в пределах изменения t от до равна 1.

Поскольку функция асимптотически приближается к оси абсцисс в пределах изменения t от до -5, а так же от +5 до считается, что единице равна площадь кривой в пределах ординат .

Значения функции даны в приложении 3, они указаны в пределах от –t до +t.

Пример : от 80 до 120

Таким образом, в 84 случаях из 100.

Складывая и вычитая площади, определенные по таблицам всегда можно получить необходимый результат.