Реферат: Управление сложными системами

Функции f ( t ) соответствует функция , ()

Одной и той же РФ соответствует множество огибающих непрерывных функций (смотри рисунок выше):

— огибающие функции.

Если ввести безразмерное время , то будет соответствовать РФ .

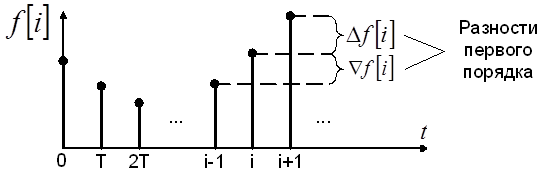
Решетчатую функцию характеризуют её разности и суммы

Разность может быть прямой () и обратной ().

.

Аналогом интеграла непрерывной функции для РФ являются её суммы:

1) Полная ;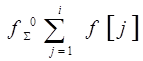

2) Неполная.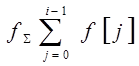

4.1.1.1.2 Разностные уравнения.

Связь между решетчатой функцией и её разностями устанавливают разностные уравнения, например:

Линейное разностное уравнение

(I΄)

Или через дискреты РФ:

(I)

Уравнение (I) — это алгоритм решения разностного уравнения при известных начальных условиях, воздействиях y и f и дискретах искомой РФ x в предшествующие моменты времени.

Коэффициенты уравнения (I) однозначно вычисляются из уравнения (I’).

4.1.1.2 Непрерывные математические модели

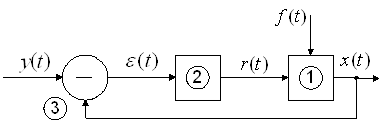
Математическая модель системы может быть получена на основе математических моделей подсистем, образующих данную систему.

4.1.1.2.1 Математическая модель системы

Рассмотрим в качестве примера непрерывную стационарную одномерную детерминированную систему с сосредоточенными параметрами