Реферат: Управление сложными системами

Объект — динамическая система, дифференциальные уравнения которой могут быть записаны следующим образом:

Х — любая линейная или нелинейная функция.

Составим уравнение регулятора:

Регулятор — также динамическая система, при этом с учётом направленности действия уравнение регулятора не будет содержать х :

Примечание. Направленность действия означает то, что объект не оказывает обратного влияния на регулятор, а только через элемент сравнения и главную обратную связь

Составим уравнение элемента сравнения:

Система уравнений , , — это математическая модель рассматриваемой системы.

В общем случае это система нелинейных дифференциальных уравнений.

4.1.1.2.2 Линеаризация математической модели

Если нелинейности системы несущественны, то ими пренебрегают, и считают модель линейной с какой-то степенью приближения.

Линейные модели используют обычно на этапе предварительного проектирования, они удобны для исследования.

Применяя соответствующий метод линеаризации, можно перейти от линейной модели к линеаризованной.

Рассмотрим один из этих методов:

он опирается на гипотезу малости отклонений “Δ”-вариаций переменных х( t ), y ( t ), r ( t ), f ( t ), от их значений, от их заданных или фиксированных значений “0” х₀ ( t ), y ₀ ( t ), r ₀ ( t ), f ₀ ( t ), , например, в установившемся состоянии.

Рассмотрим уравнение объекта :

Полагая и , решения уравнения можно найти в виде , а уравнения в виде , тогда:

Лекция №6. 26.02.2003

Если X непрерывная и однозначная функция, то её можно разложить в ряд Тейлора в окрестности некоторых точек х₀ , r ₀ , f ₀ :

.

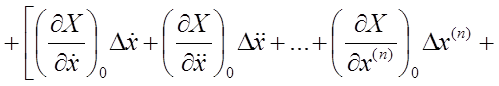
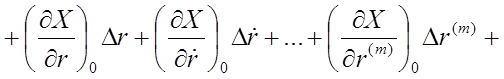
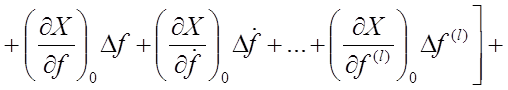
Пренебрегая членами ряда порядка выше первого (из-за их малости), с учётом частного случая (в установившемся состоянии после переходного режима при , ) после преобразований в операторной форме это уравнение () можно записать в следующем виде: