Реферат: Знакочередующиеся и знакопеременные ряды

ε = , найдется такой номер N , начиная с которого будет выполняться неравенство

,

откуда или что тоже,

.

Отсюда получаем

для .

Таким образом, все члены ряда, начиная с , меньше соответствующих членов сходящегося ряда . По признаку сравнения ряд

сходится, а значит сходится и ряд(1).

2)Пусть . Тогда, начиная с некоторого номера N для всех n > N , будет выполняться неравенство , или

.

Следовательно,

И ряд (1) расходится. ►

Замечание. Если , то ряд (1) может как сходиться, так и расходиться.

Примеры. Исследовать на сходимость следующие ряды:

1. .

◄ Имеем

, ;

.

Ряд сходится. ►

2.

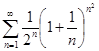
◄ Здесь

, ;

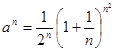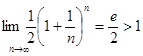
Ряд сходится. ►

3. Интегральный признак сходимости ряда

Теорема 3 (интегральный признак сходимости). Пусть функция f(x) определена, непрерывна, положительна и не возрастает на луче . Тогда:

1) числовой ряд сходится, если сходится несобственный интеграл