Реферат: Знакочередующиеся и знакопеременные ряды

,

◄ Так как общий член ряда

то в качестве функции возьмем

, где x ≥ 4.

Тогда

==

==

=.

Так как несобственный интеграл

сходится, то сходится и исходный ряд. ►

В случае сходимости ряда метод, примененный при доказательстве интегрального признака сходимости, позволяет получить оценку погрешности, возникающей при замене суммы ряда частичной суммой.

Пусть функция f(x) удовлетворяет условиям теоремы 9, ряд

сходится и его сумма равна S. Можно показать, что в этом случае будет сходиться и несобственный интеграл

.

Пользуясь неравенством

,

оценим остаток Rn заданного ряда, Имеем

.

Итак,

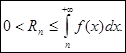
Таким образом, погрешность, получаемая при замене суммы S сходящегося ряда

его n-й частичной суммой Sn , не превосходит интеграла .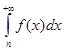

Пример 5. Установить сходимость ряда

и оценить погрешность при замене его суммы S5.

◄ Здесь