Реферат: Знакочередующиеся и знакопеременные ряды

В силу интегрального признака ряд сходится. Обозначим сумму этого ряда через S и будем считать, что

S ≈ S5. Тогда

S ≈ S5 ==

Оценим погрешность R5. Имеем

►

Замечание. Обозначение

понимается так

===

=.

Пример 6. Оценить n-й остаток сходящегося ряда

где p>1.

◄ Имеем

= = = . ►

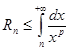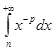4 Знакочередующиеся ряды. Признак Лейбница

Определение. Числовой ряд

a1 – a2 + a3 – … + (– 1) n - 1an + … ,

где все числа an положительны, называется знакочередующимся.

Пример. Ряд

является знакочередующимся, а ряд

знакочередующимся не является.

Для знакочередующихся рядов имеет место следующий признак сходимости, который носит название признака Лейбница.

Теорема 4 (признак Лейбница). Пусть в знакочередующемся ряде

a1 – a2 + a3 – …

числовая последовательность { an } убывает,