Шпаргалка: Методы кинематического исследования механизмов

Под степенью подвижности кинематической цепи понимается ее наибольшее число степеней свободы относительно условно неподвижной стойки.

Для плоских механизмов, звенья которых движутся в плоскостях, параллельных между собой, число степеней свободы определяется по формуле Чебышева: W = 3n – 2p₁ – p₂ . Данная формула является структурной формулой плоских механизмов.

Пассивные связи и избыточные подвижности

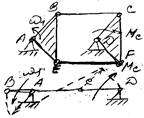
M_C –момент сопротивления движению. Переход механизма из одной сборки в другую (механизм неправильно спроектирован). Усовершенствованный механизм с дополнительными звеньями не меняет сборки при работе.

W = 3n–2p₁ =3×4–2×6 = 0. Это говорит о том, что механизм не вращается. Но на самом деле он вращается, но есть пассивная связь EF, не добавляющая степеней свободы механизму.

Аналитический метод кинематического исследования механизмов. Аналоги скоростей и ускорений

Кинематическое исследование механизма, т.е. изучение движения звеньев механизма без учета сил, обусловливающих это движение, состоит в основном в решении трех следующих задач:

1) определение перемещений звеньев и траекторий, описываемых точками звеньев; 2) определение скоростей отдельных точек звеньев и угловых скоростей звеньев; 3) определение ускорений отдельных точек звеньев и угловых ускорений звеньев. В аналитической форме функция перемещений, скоростей или ускорений задаются в виде функции, связывающей перемещение или угол поворота ведущего звена со временем, в зависимости от того, какую пару образует ведущее звено. Рассмотрим Группу Ассура 3-го вида:

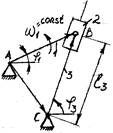
Используется метод замкнутых векторных контуров.

1)`A`B =`A`C + `C`B,

óС_х +ℓ₃ cosj₃ = B_x

ôC_y +ℓ₃ sinj₃ = B_y

ℓ₃ =Ö[(B_x –C_x )² +(B_y –C_y )² ], j₃ = arctg[B_y –C_y )/(B_x –C_x )],

откуда B_x =ℓ_AB cosj₁ ,

B_y = ℓ_AB sinj₁ .

2)Угловая скорость w_k этого звена может быть представлена так: w₃ = dj₃ /dt – угловая скорость, j¢₃ = dj₃ /dj – безразмерная угловая скорость звена 3, называемая аналогом угловой скорости.

3)Угловое ускорение определяется формулой e_k = dw_k /dt, тогда d² j₃ /dj₁ ² = j₃ ¢¢ называется аналогом углового ускорения. Скорость поступательного движения какого-либо звена равна V = dS/dt , величина

dS/dt=dS/dj×dj/dt,

где dS/dt – аналог скорости, имеющий размерность длины. Т.е V = S¢×w (уравнение связи), где S¢–аналог скорости звена. Продифференцировав это выражение по времени, получаем

a_m = dV/dt = d(S¢w)/dt = w×dS¢/dt + S¢dw/dt = w² S¢¢ + eS¢.

Величина a = S¢¢=d² S/dj₂ есть аналог ускорения, имеющий также размерность длины.

Графический метод кинематического анализа плоских рычажных механизмов. Два метода разложения движения. Построение планов скоростей и ускорений. Теорема о подобии

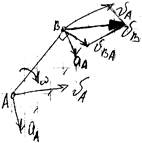
1-й способ разложения движения (применяется когда известно движение одной точки звена и требуется определить движение другой точки того же звена):

V_B = V_A +V_BA ,

где V_A –переносная скорость, V_BA – относительная скорость (скорость точки В по отношению к точке А),