Шпаргалка: Методы кинематического исследования механизмов

где a_A – переносное ускорение, a_BA ⁿ и a_BA ^t – относительные ускорения. 2-й способ (применяется когда известно движение звена и надо определить движение второго звена и эти два звена образуют поступательную пару):

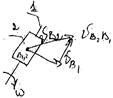
Точки B₂ и B₁ совпадают, V_{B 2} = V_{B 1} + V_{B 2 B 1} , где V_{B 1} – переносная (вращательная) скорость, V_{B 2 B 1} – относительная скорость (поступательная); a_{B 2} =a_{B 1} + a_{B 2 B 1} ^k + a_{B 2 B 1} ^r , a_{B 1} – переносное ускорение, a_{B 2 B 1} ^k (поворотное) и a_{B 2 B 1} ^r (реактивное)– относительные.

Теорема о подобии (применяется для точек одного звена, когда известны скорости, ускорения двух точек этого звена): относительные скорости и ускорения точек одного и того же звена образуют на планах скоростей и ускорений фигуры, подобные одноименной фигуре на схеме механизма. Эти фигуры сходственно расположены, т.е. при чтении буквенных обозначений их вершин в одинаковом направлении буквы следуют в одинаковом порядке.

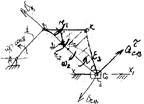
Построение плана скоростей: P_V - полюс плана скоростей ( в этой точке скорость равна 0), V_{B 1} = w₁ ℓ_AB [м/с], w1 = 2pn/60 =pn/30, m_V = V_B /(p_V b) – масштабный коэффициент скорости,

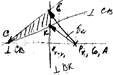
óV_C = V_B + V_CB (^CB)

ôV_CB = V_C0 (=0)+V_CDC0 (|| x-x₁ ),

w₂ = V_CB /ℓ_CB = (cb)m_V /ℓ_CB , VC = (P_V c)m_V .

Построение плана ускорений: a_B = a_B ⁿ = w₁ ℓ_AB [м/с² ]. p = P_V – полюс плана ускорений,

m_a = a_B ⁿ /(pb₁ ) [м/(с² мм)].

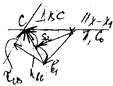
a_C = a_B + a_CB ⁿ + a_CB ^t

a_C3 = a_C0 + a_C3C0 ^K (=0)+ a_C3C0 ,

a^K = 2V_отн w_пер – Кориолисово ускорение, a_CB ⁿ =w₂ ² ℓ_{B С} = V_BC /ℓ_CB =

= (bc×m_V )² /ℓ_BC , n_BC = a_BC ⁿ /m_a , e_i = a_i ^t /ℓ_i ,

e₂ = a_CB ^t /ℓ_CB = (t_CB )×m_a /ℓ_CB .

Силовой расчет. Задачи и методы, допущения

Кинетостика – задача силового расчета (на основе обыкновенных уравнений равновесия твердых тел.). Перед кинетостатикой ставится две задачи: 1) определение усилий к кинематических парах; 2) определение уравновешивающей силы (F_ур ). Силовой раcчет провидится по методу Даламбера (если ко всем внешним действующим на звено механизма силам присоединить силы инерции, то под действием всех этих сил можно звено рассматривать условно находящимся в равновесии, SF_i =0): SF_xi =0, SF_yi = 0, SF_zi = 0, силы трения при этом не учитываются.

Условие статической определимости системы

3n=2p₁ +p₂ – усилие статической определимости, число усилий = число неизвестных. Чаще 3n = 2p₁ , т.к. p₂ = 0, условие существований групп Ассура (DW=3n–2p₁ = 0).

Определение сил инерции и моментов от сил инерции

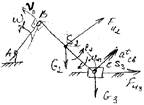
S₂ – центр масс 2-го звена

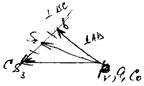
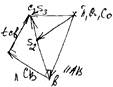
F_И2 = –m₂ ×a_{S 2} = – m₂ (nS₂ )m_a , M_И2