Шпаргалка: Методы кинематического исследования механизмов
w2 ср (1–d)=2mT /my × tgymin .
Типы и виды механизмов с высшими кинематическими парами
Среди механизмов с высшими кинематическими парами наибольшее распространение получили зубчатые, кулачковые, фрикционные, мальтийские и храповые механизмы.
В зубчатых передачах различают внешнее, внутренне и реечное зацепление. В зависимости от расположения осей могут быть с параллельными осями (цилиндрические), с пересекающимися осями (конические) и со скрещивающимися осями или гиперболоидные передачи (винтовые, червячные).
В кулачковых механизмах высшая пара образована звеньями, называемыми кулачок и толкатель (звено 1 и 2). Замыкание силовое, с помощью пружины. Форма входного звена – кулачка определяет закон движения выходного звена – толкателя.
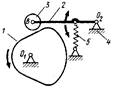
В фрикционном механизме передача вращательного движения осуществляется посредством трения между звеньями, образующими высшую кинематическую пару. Простой фрикционный механизм состоит из двух вращающихся круглых цилиндров 1,2 и стойки 3. Силовое замыкание высшей пары осуществляется пружинами. При постоянной угловой скорости диска 1 посредством перемещения колеса 2 вдоль своей оси можно плавно изменять его угловую скорость и даже направление вращения.
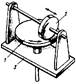
Мальтийский механизм преобразует непрерывное вращение входного звена – кривошипа 1 в прерывистое вращение выходного звена – креста 2. Механизм имеет стойку 3 и высшую пару, образованную цевкой В кривошипа и пазом креста.
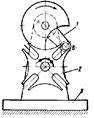
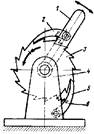
Храповой механизм с ведущей собачкой и стойкой 4 служит для преобразования возвратно-вращательного движения коромысла 1 с собачкой 2 в прерывистое вращательное движение храпового колеса 3. Собачка 5 с пружиной 6 не дает колесу вращаться в обратную сторону. Высшая КП здесь образована собачкой и храповым колесом.
Эвольвента и ее свойства. Свойства эвольвентного зацепления. Основная теорема зацепления. Зубчатые меха низмы
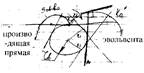
Эвольвента – это траектория некоторой фиксированной точки прямой, катящейся без скольжения по окружности. Окружность, по которой без скольжения катится эвольвента называется основной . Основные свойства эвольвенты: 1)нормаль любой точки эвольвенты касается основной окружности, т.е. явл. производящей прямой; 2)отрезок производящей прямой от точки эвольвенты до точки касания равен радиусу кривизны; 3)эвольвента не бывает внутри основной окружности.

k1 – точка касания, a– угол профиля
k0 k1 =k1 k0 ¢, rb ×(q+a)=rb ×tga, q=tga–a, inva=tga–a – уравнение эвольвенты, ry ×cosa=rb , ry =rb /cosa. Основная теорема зацепления (т. Виллиса): w1 /w2 =p2 p / p1 p

Vk1 ¢=Vk1 cosa1 = r1 w1 cosa1
Vk2 ¢=Vk2 cosa2 = r2 w2 cosa2
O1 L1 w1 = O2 L2 w2 , w1 /w2 = O2 L2 / O1 L1 .
Теорема: нормаль в точке касания в высшей кинематической паре делит межосевое расстояние (O1 O2 ) на части обратно пропорциональные угловым скоростям. Основные свойства эвольвентного зацепления: 1)Эвольвентное зацепление обеспечивает постоянство передаточных отношений:
w1 /w2 =O2 p/O1 p = rw2 /rw1 =rb2 /rb1 .
2)Прямая N1 N2 является общей касательной Þ точка соприкосновение зубьев всегда лежит на ней и тогда она называется прямой зацепления, aw – угол зацепления, который всегда равен 20°. 3) Если одно из колес будет увеличиваться в ¥ размерах, то профиль зуба будет прямой), то она превратится в в зубчатую рейку и будет перемещаться поступательно.
Элементы геометрии прямозубых зубчатых колес. Угловой шаг, окружный шаг, модуль, окружности: основная, делительная, впадин и вершин зубьев

p–окружной шаг, py – шаг по промежуточному радиусу, ra – радиус окружности внешних зубьев, rf – радиус окружности впадин между зубьями, r – радиус делительной окружности, ry – радиус промежуточной окружности,