Шпаргалка: О теории вероятностей

Следствие2.

Если события А₁ ,А₂ , …, А_n независимы и имеют одинаковую вероятность появиться (Р(А₁ )=Р(А₂ )=…Р(А_n )= р, Р(А_i )= 1-р=q ), то вероятность появления хотя бы одного из них равна Р(А)=1-qⁿ .

5. Формулы полной вероятности и вероятности гипотез

Пусть событие А может наступать только одновременно с одним из попарно несовместных событий Н₁ , Н₂ , ..., Н_n , образующих полную группу. Тогда вероятность события А определятся по формуле полной вероятности:

Р(А) = Р(Н₁ )*P(А/Н₁ ) + Р(Н₂ )*Р(А/Н₂ ) +...+ Р(Н_n )*Р(А/Н_n ), или Р(А)= Σ Р(Н_i )*Р(А/Н_i ),

где события Н₁ ,Н₂ , ...,Н_n , - гипотезы, a P(A/H_i ) - условная вероятность наступления события А при наступлении i-ой гипотезы (i=1, 2,..., n).

Условная вероятность гипотезы Н_i при условии того, что событие А произошло, определяется по формуле вероятности гипотез или формуле Байеса (она позволяет пересмотреть вероятности гипотез после наступления события А):

Р(Н_i /А)=(P(H_i )*P(A/H_i ))/P(A).

6. Формула Бернулли

Пусть некоторый опыт повторяется в неизменных условиях n раз, причём каждый раз может либо наступить (успех), либо не наступить (неудача) некоторое событие А, где Р(А) = р - вероятность успеха, Р(А)=1-р= q - вероятность неудачи. Тогда вероятность того, что в к случаях из n произойдёт событие А вычисляется по формуле Бернулли

P_n (K) = C^k _n -p^k -q^n-k .

Условия, приводящие к формуле Бернулли, называются схемой повторных независимых испытаний или схемой Бернулли. Так как вероятности Р_n (к) для раз личных значений к представляют собой слагаемые в разложении бинома Ньютона

(p+q)ⁿ =C⁰ _n *p⁰ *qⁿ +C¹ _n *p¹ *q^{n -1} +…+C^k _n *p^k *q^{n - k} +…+Cⁿ _n *pⁿ *q⁰ ,

то распределение вероятностей P_n (k), где 0≤k≤n, называется биноминальным.

Если в каждом из независимых испытаний вероятности наступления события А разные, то вероятность наступления события А к раз в n опытах определяется как коэффициент, при к-ой степени полинома

φ_n (Z)=Π(q_i +p_i Z)=a_n Zⁿ +a_{n -1} Z^{n -1} +…+a₁ Z₁ +a₀ , где φ_n (Z) - производящая функция.

Невероятнейшее число наступивших событий в схеме Бернулли - к_о (к₀ c К) определяется из следующего неравенства: np-q≤k₀ ≤np+p.

7. Локальная формула Муавра-Лапласа

Если npq>10 , то

где вероятность р отлична от 0 и 1 (р→0,5), х =(k-np)/√npq.

Для облегчения вычислений функция

представлена в виде таблицы (прил.1).

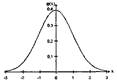
φ(х) - функция вероятности нормального распределения (рис. 6) имеет следующие свойства:

1) φ(х)-четная;

2) точки перегиба х = ± 1;

3) при х≥5, φ(х)→0, поэтому функция φ(х) представлена в виде таблицы для 0≤х≤5 (прил.1).