Шпаргалка: О теории вероятностей
8. Интегральная теорема Муавра-Лапласа.
При больших значениях n , для вычисления вероятности того, что произойдет от к1 , до к2 событий по схеме
![]()
Бернулли, используется интегральная формула Муавра-Лапласа
Pn (k1 ≤k≤k2 )=Ф(x2 )- Ф(x1 ),
где x1 =(k1 -np) /(√npq), x2 =(k2 -np)/(√npq), Ф(x) – функция Лапласа. (рис.7)
Ф(х) имеет следующие свойства:
1. Ф(-х)= -Ф(х) - функция нечетная, поэтому достаточно изучать её для неотрицательных значений х
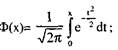
2. Функция Ф(х) возрастает на всей числовой оси;
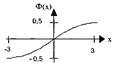
Рис. Функция Лапласа
3. При х≥5, Ф(х)→1/2 (y = 0,5 горизонтальная асимптота при х>0), поэтому функция представлена в виде таблицы Для 0≤х≤5 (прил.1).
4. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях не более чем на некоторое число ε>0
![]()
9. Формула Пуассона
Если npq<10 и р<0,1, то
![]() где λ=np.
где λ=np.
10. Случайные величины и их виды
Случайной величиной (СВ) называют такую величину, которая в результате опыта может принимать те или иные значения, причем до опыта мы не можем сказать какое именно значение она примет. (Более точно, СВ - это действительная функция, определенная на пространстве элементарных событий Q). Случайные величины обозначаются последними буквами латинского алфавита - X,Y,Z. Случайные величины могут быть трех типов: - дискретные, - непрерывные, - смешанные (дискретно-непрерывные). Дискретная случайная величина (ДСВ) может принимать конечное или бесконечное счетное число значений. Непрерывная случайная величина (НСВ) в отличие от ДСВ принимает бесконечное несчетное число значений. Например мишень имеет форму круга радиуса R. По этой мишени произвели выстрел с обязательным попаданием. Обозначим через Y расстояние от центра мишени до точки попадания, Ye [0; R]. Y - непрерывная случайная величина, так как она принимает бесконечное несчетное число значений.
Пусть X - дискретная случайная величина, которая принимает значения х1 , х2 , ...,хn ,... с некоторой вероятностью рi , где i = 1, 2, ..., n,... Тогда можно говорить о вероятности того, что случайная величина X приняла значение хi : рi =Р(Х=хi ).
ДСВ может также представляться в виде многоугольника распределения – фигуры, состоящей из точек, соединенных отрезками. Над СВ устанавливаются операции сложения и умножения.
Суммой двух СВ X и Y наз-ся случайная величина, которая получается в рез-те сложения всех значений случайной величины X и всех значений СВ Y, соответствующие вероятности перемножаются. Произведением двух СВ X и Y наз-ся СВ, которая получается в рез-те перемножения всех значений СВ X и всех значений СВ Y, соответствующие вероятности перемножаются.
11. Математическое ожидание
Математическим ожиданием М(Х) ДСВ X называется среднее значение случайной величины:
![]()
Или иначе, М(Х) - это сумма парных произведений случайной величины на соответствующую вероятность:
![]()
Мода Мо (Х) распределения - это значение СВ, имеющее наиболее вероятное значение.