Шпаргалка: О теории вероятностей
Отсюда, по формуле классического определения вероятности, P(A)= (Сm M Сn - m N - M )/ Cn N
Ограничения на параметры: М≤N, m≤n; m = m0 , m0 +1, m0 +2,..., min(M,n), где m0 =max{0, n-(N-M)}. Случайная величина Х, распределенная по гипергеометрическому закону распределения (при т=0,1,2,3,...,М), имеет вид:
![]()
Гипергеометрический закон определяется тремя параметрами N, М, n. При n<0,1N этот закон стремится к биномиальному.
Замечание.
1. В теории вероятностей различают две основные схемы: выбора элементов с возвращением каждый раз обратно и выбора без возвращения, которые описываются соответственно биномиальным и гипергеометрическим законами.
2. Геометрический закон описывает схему повторения опытов (в каждом из которых может наступить или не наступить событие А: Р(А)=р, q=l-p), до первого появления события А, то есть фактически это отрицательное биномиальное распределение при m=1.
16. Одинаково распределённые, взаимонезависимые дискретные случайные величины
СВ называют одинаково распределенными, если они имеют одинаковые законы распределения. Поэтому у них совпадают числовые характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение.
Пусть X1 , Х2 ,..., Хn одинаково распределенные, взаимонезависимые ДСВ, тогда:
M(X1 ) = М(Х2 ) = ... = М(Хn ) = М(Х), D(X1 ) = D(X2 ) = ...= D(Xn )=D(X).
Рассмотрим характеристики их средней арифметической X = (X1 +X2 +…+Xn )/n:
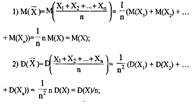
![]()
![]()
-стандартное отклонение СВ X.
Дисперсия относительной частоты (m/n) появления события А в n независимых испытаниях (в каждом из которых событие А появляется с вероятностью равной р, и не появляется с вероятностью q= 1-р; m-число появлений события А в серии из n испытаний), определяется по формуле
15. Дифференциальная функция распределения и ее свойства
СВ X непрерывна, если ее интегральная функция непрерывна на всей числовой оси. СВ X непрерывна и имеет дифференциальную функцию, если ее интегральная функция непрерывна и дифференцируема всюду, за исключением конечного числа точек на любом конечном промежутке.
Дифференциальной функцией (функцией плотности вероятности) СВ X называется производная ее функции распределения: f(x)=F'(x).
С помощью дифференциальной функции можно получить формулу вероятности попадания СВ X в заданный интервал:
![]()
Свойства дифференциальной функции:
). f(x)≥0;
![]()
![]()
16. Числовые характеристики непрерывных случайных величин
1) Математическое ожидание НСВ X определяется по формуле
М(Х)= ∫xf(x)dx. (2.7.1)
Если НСВ X определена на интервале (а; b), то