Шпаргалка: О теории вероятностей

Вероятность заданного отклонения. Правило трех сигм.

Найдем вероятность того, что случайная величина X, распределённая по нормальному закону, отклонится от математического ожидания М(Х)=а не более чем на величину ε>0.

Р(|х-а|<ε)= Р(-ε< х-а<+ε) = Р(а-ε<х< а+е) =Ф^* ((a+ε-a)/σ)-Ф^* ((a-ε-a)/σ)=Ф^* (ε/σ)-(1-Ф^* (ε/σ))=2Ф^* (ε/σ)-1.

Или, используя функцию Лапласа:

P(|X-a|<ε)=2Ф(ε/σ).

Найдём вероятность того, что нормально распределённая СВ X отклонится от M(X)=a на σ, 2σ, 3σ:

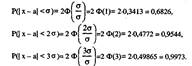
Отсюда следует правило Зσ. если случайная величина X имеет нормальное распределение, то отклонение этой случайной величины от ее математического ожидания по абсолютной величине не превышает утроенное среднее квадратическое отклонение (Зσ).

20. Многомерные случайные величины

В практических задачах приходится сталкиваться со случаями, когда результат описывается двумя и более случайными величинами, образующими систему случайных величин (случайный вектор). Например, точка попадания снаряда имеет две координаты: х и у, которые можно принять за систему случайных величин, определенных на одном и том же пространстве элементарных событий Ω.

Закон распределения дискретной двумерной случайной величины можно представить в виде таблицы, характеризующей собой совокупность всех значений случайных величин и соответствующих вероятностей: