Математика / Шпаргалка: Ответы на экзаменационные билеты по высшей математики

Шпаргалка: Ответы на экзаменационные билеты по высшей математики

∫f(x)dx; ∫f(x)dx ? ∫g(x)dx

№31 Дифференциальные однородные уравнения первого порядка.

ДУ первого порядка называется однородным, если оно может быть представлено в виде y’ = g (y/x).

Однородное ДУ преобразуется в уравнение с разделяющимися переменными при помощи замены z=y/x; y=z*x, то y’=z’x+z, поэтому уравнение y’=g(y/x) преобразуем к виду z’x+z=g(z); dz*x/dx=g(z)-z; dz\(g(z)-z)=dx/x.

Найдя его общее решение следует заметить в нем z на y/x.

Однородное ДУ часто задается в дифференциальной форме: P(x;y)dx+Q(x;y)dy=0.

ДУ будет однородным, если P(x;y) и Q(x;y) – однородные функции одинакового порядка.

Переписав уравнение в виде dy/dx=-P(x;y)/Q(x;y) и переменив в правой части рассмотренное выше преобразование получим уравнение y’=g(y/x).

При интегрировании уравнения P(x;y)dx+Q(x;y)dy=0 нет необходимости предварительно приводить их к виду y’=g(y/x): подстановка z=y/x сразу преобразует уравнение P(x;y)dx+Q(x;y)dy=0 в уравнение с разделяющимися переменными.

№32 Степенные ряды

Степенным рядом называется ряд вида а₀ +а₁ х+а₂ х² +…+a_n xⁿ +…, а также ряд более общего вида а₀ +а1(х-х₀ )+а₂ (х-х₀ )² +…+a_n (x-х₀ )ⁿ +…, где х₀ – постоянная величина. О первом ряде говорят, что он расположен по степеням х, во втором – что он расположен по степеням х-х_0.

Постоянные а₀ , а₁ , …, а_n , … называются коэффициентами степенного ряда.

Степенной ряд всегда сходится при х=0.

№33 Кривые второго порядка на плоскости (эллипс, гипербола, парабола).

Линии, определяемые уравнениями второй степени относительно переменных x и y, т.е. уравнениям вида Ах² +2Вху+Су² +2Вх+2Еу+F=0 (А² +В² +С² ≠0), называются кривыми 2-го порядка.

Эллипс.

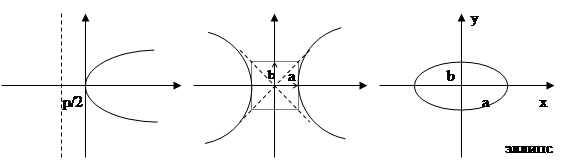х² /а² +у² /b² =1