Учебное пособие: Аналитическая геометрия

Рис.12

1.3.2 Методы получения уравнения прямой

Уравнение прямой, проходящей через две данные точки

Пусть прямая проходит через две данные точки M₁ (x₁ ; y₁ ) и M₂ (x₂ ; y₂ ), тогда для нахождения уравнения прямой используется выражение

Пример 8 (получение уравнения прямой)

Получить уравнение прямой, проходящей через точки M₁ (3; 1) и M₂ (5; 4). Представить эскиз.

Решение :

Итак, имея ввиду последний результат, определяемся со значениями входящих в него величин:

x₁ = 3; y₁ = 1;

x₂ = 5; y₂ = 4,

тогда

Т.е. ответ на первую часть задачи – уравнение прямой имеет вид

В силу чего, эскиз получается мгновенно: ось Oy пересекается в точке , а эскиз – на рисунке 13

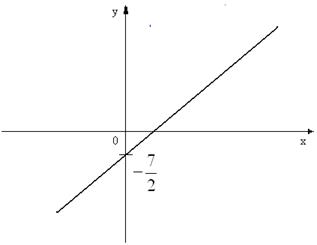
Рис.13

Угол между двумя прямыми

Пусть две прямые заданы своими уравнениями с угловыми коэффициентами:

y = b₁ + k₁ ∙x и y = b₂ + k₂ ∙x ,

(см. рисунок 14)

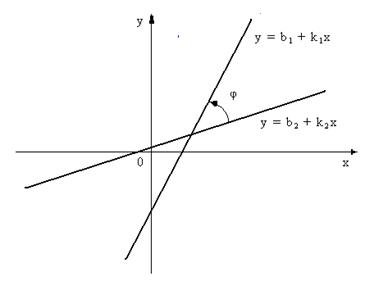
Рис.14

тогда угол α между ними определяется выражением

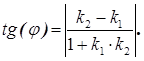
Замечание : при этом находится значение наименьшего из четырех углов, образованных пересекающимися прямыми.

Из приведенного выражения существует два весьма важных следствия: условия параллельности и перпендикулярности прямых.

Условие параллельности двух прямых