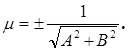Учебное пособие: Аналитическая геометрия

Рассмотрим рисунок 16

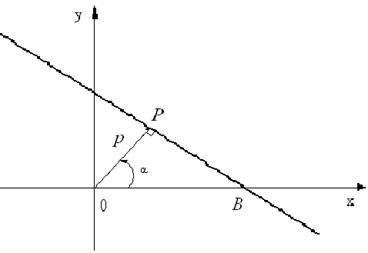
Рис.16

На рисунке – отрезок ОР – нормаль (откуда и название – «нормальное уравнение прямой») проведенная из начала координат до пересечения с прямой (угол ОРВ – прямой); угол α образован нормалью к прямой и положительным направлением оси Ox; длина отрезка ОР = р.

Тогда нормальное уравнение прямой имеет вид

Отклонение и расстояние точки от прямой

Если точка, то подстановка ее координат в общее уравнение прямой

A∙x + B∙y + C = 0,

не даст нам верного равенства:

A∙x^* + B∙y^* + C 0.

И это все, а вот подстановка тех же координат в нормальное уравнение прямой

Величина называется отклонением точки от прямой, причем (что очень важно) имеет место

Теорема об отклонении точки от прямой

Если точка М^* (x^* ; y^* ) прямой не принадлежит, то ее отклонение от прямой определяется выражением

Причем

- - расстояние от точки до прямой;

- если то точка М^* и начало координат расположены по разные стороны прямой ;

- если , то точка М^* и начало координат расположены по одну сторону от прямой .

Приведение прямой к нормальному виду (нормализация уравнения прямой)

Для приведения общего уравнения прямой

A∙x + B∙y + C = 0

к нормальному виду используется процедура нормализации:

Шаг 1

Вычисление нормирующего множителя