Учебное пособие: Аналитическая геометрия
y = b1 + k1 ∙x и y = b2 + k2 ∙x,
параллельны при условии
k1 = k2 .
(Что для нас не удивительно – см. пример 11: прямые 1,2 и 3.4).
Условие перпендикулярности двух прямых
Две прямые, определенные уравнениями с угловым коэффициентом
y = b1 + k1 ∙x и y = b2 + k2 ∙x,
перпендикулярны при условии
k1 ∙k2 = -1 или ![]() .
.
Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом
Если известно, что прямая проходит через данную точку M(x1 ; y1 ) c данным угловым коэффициентом k, то для нахождения уравнения этой прямой используется выражение
y = y1 + k∙(x – x1 ).
Пример 9 (о нахождении проекции точки на прямую)
Найти проекцию точки Р(4; 9) на прямую, проходящую через точки А(3; 1) и В(5; 2).
Решение :
Прежде всего: найти проекцию точки, это значит найти координаты «тени» этой точки на прямую.
Задача решается в три шага:
- находится уравнение прямой, проходящей через точки А и В;
- находится уравнение прямой, проходящей через точку Р, перпендикулярно прямой АВ;
- находятся координаты точки пересечения прямой, проходящей через точку Р и прямую АВ.
Шаг 1
Уравнение прямой АВ ищем посредством выражения для нахождения уравнения РїСЂСЏРјРѕР№, проходящей через РґРІРµ данные точки :
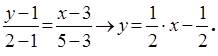
Шаг 2
Искомая прямая проходит через точку Р(4; 9) с угловым коэффициентом, определяемым из условия перпендикулярности прямых (поскольку точка, являющаяся проекцией точки Р на прямую АВ есть результат пересечения прямой перпендикулярной прямой АВ, проходящей через точку Р).
Тогда угловой коэффициент искомой прямой k: