Учебное пособие: Аналитическая геометрия

y – 9 = -2∙(x– 4) → y = - 2∙x + 17.

Т.о., искомая прямая определяется уравнением

y = - 2∙x + 17.

Шаг 3

Проекцию точки Р на прямую АВ находим как результата пересечения найденной прямой и прямой АВ

,

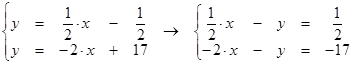Решая полученную систему окончательно находим ответ:

координаты точки пересечения (7; 3).

1.3.3 Другие формы уравнения прямой

Общее уравнение прямой

Общим уравнением прямой называется уравнение вида

A∙x + B∙y + C = 0.

«Общим» это уравнение называется потому, что из него можно получить все три формы уравнения прямой.

Так, например можно получить уравнение прямой с угловым коэффициентом:

т.е., в этом случае угловой коэффициент .

Общее уравнение прямой потому и называется «общим», что из него можно получить не только уравнение с угловым коэффициентом, но и еще две формы уравнения прямой, каждая из которых оказывается полезной при решении своего класса задач.

Итак, пусть дано общее уравнение прямой

A∙x + B∙y + C = 0,

причем , тогда

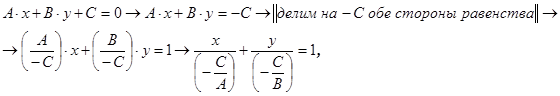
вводя обозначения

откуда окончательно получаем

Уравнение прямой в отрезках

где a и b – величины отрезков (откуда и название!), отсекаемых прямой соответственно на оси Ox и оси Oy (cм. Рис.15).

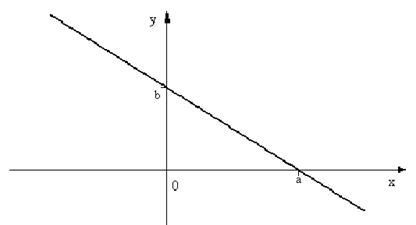
Рис.15