Учебное пособие: Исследование функций и построение их графиков

Тема 1. Предел функции

Число А называется пределом функции при , стремящимся к , если для любого положительного числа (>0) найдется такое положительное число >0 (зависящее в общем случае от ), что для всех , не равных и удовлетворяющих условию xx<, выполняется неравенство xА x<.

Для предела функции вводится обозначение =А.

Пределы функций обладают следующими основными свойствами:

Функция не может иметь более одного предела.

Если = С (постоянная), то С.

Если существует А, то для любого числа верно:

Если существуют А и В, то = АВ, а если В0, то

.

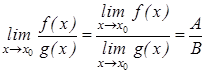Операция предельного перехода перестановочна с операцией вычисления непрерывной функции, т. е. справедлива формула

Если функция непрерывна в точке , то искомый предел равен значению функции в этой точке, т.е. он находится непосредственной подстановкой предельного значения переменной вместо аргумента :

Функция ( называется бесконечно малой величиной при , если ее предел равен нулю: Функция называется бесконечно большой величиной при , если

Пример 1. 9.

Пример 2. .

В рассмотренных примерах предел находился сразу: в виде числа или символа (бесконечность). Но чаще при вычислении пределов мы встречаемся с неопределенностями, когда результат нахождения предела не ясен, например, в случае отношения двух бесконечно малых функций (условное обозначение ) или бесконечно больших ().Кроме названных встречаются неопределенности вида

Для раскрытия неопределенностей используются специальные приемы и два следующих предела, которые играют особую роль в математике и поэтому называются замечательными:

- первый замечательный предел

-второй замечательный предел (число Эйлера).

Пример 3. .

Решение. Непосредственной подстановкой убеждаемся, что имеем дело с неопределенностью вида :

.

Для раскрытия неопределенности разложим числитель и знаменатель на множители. Найдем корни многочлена, стоящего в числителе. Для этого составим уравнение второй степени и найдем его решение:

Тогда для квадратного трехчлена справедливо разложение на множители

.

Аналогичные действия выполним для многочлена, стоящего в знаменателе.

Уравнение имеет решения

--> ЧИТАТЬ ПОЛНОСТЬЮ <--