Учебное пособие: Исследование функций и построение их графиков

Тогда размер вклада за лет при непрерывном начислении процентов () сводится к нахождению предела

.

Здесь при решении использовался второй замечательный предел.

Подставляя исходные числовые данные задачи, получаем

(ден. единиц).

Вопросы для самопроверки

Дайте определение предела функции в точке.

Назовите основные свойства пределов функций.

Какие виды неопределенностей встречаются при нахождении пределов?

Какие пределы называются замечательными?

Какие функции называют бесконечно малыми?

Задачи для самостоятельной работы

Найти пределы следующих функций:

Номер варианта	А)	Б)
1
2
3
4
5
6
7
8
9
10

Таблица 1.

Тема 2. Производная функции

Приращением функции в точке , соответствующим приращению аргумента , называется число .

Производной функции в точке называется предел отношения приращения функции к приращению аргумента при , если этот предел существует, и обозначается:

.

Нахождение производной функции называется дифференцированием этой функции. Если функция имеет в точке конечную производную, то функция называется дифференцируемой в этой точке.

Важнейшими правилами дифференцирования являются следующие.

Производная постоянной равна нулю: .

Постоянный множитель выносится за знак производной

.

Производная суммы (разности) функций равна сумме (разности) производных этих функций

.

Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго

.

Производная частного двух дифференцируемых функций находится по формуле

.
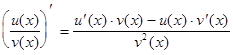