Учебное пособие: Исследование функций и построение их графиков

Вычислить приближённое значение , заменив в точке приращение функции ее дифференциалом.

Таблица 4.

Номер варианта
1	3	502	512
2	4	267	256
3	5	234	243
4	6	685	729
5	7	142	128
6	3	349	343
7	4	605	625
8	5	255	243
9	6	773	729
10	7	156	128

Тема 4. Исследование функций и построение их графиков

Если функция одной переменной задана в виде формулы , то областью ее определения называют такое множество значений аргумента , на котором определены значения функции.

Пример 1. Значение функции определены только для неотрицательных значений переменной : . Отсюда область определения функции будет полуинтервал [4;).

Пример 2. Функция

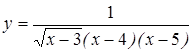
не определена при таких значениях аргумента , когда либо знаменатель равен нулю (), либо подкоренное выражение отрицательно (<3). Тогда областью определения служит множество, являющееся объединением интервалов (3;4)(4;5) (5;).

Пример 3. Функция определена только на отрезке [-1;1], так как значение тригонометрической функции удовлетворяют неравенству: -11.

Функция называется четной, если для любых значений из области ее определения выполняется равенство

,

и нечетной, если справедливо другое соотношение: . В других случаях функцию называют функцией общего вида.

Пример 4. Пусть . Проверим:

.

Таким образом, эта функция является четной.

Для функции верно: . Отсюда эта функция нечетная.

Их сумма является функцией общего вида, так как не равна и .

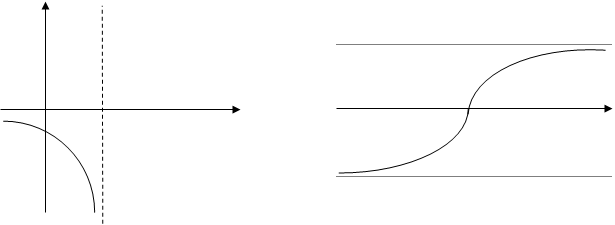
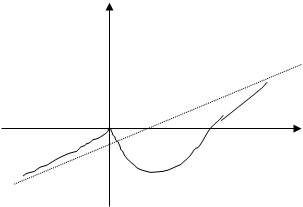
Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точки (;) плоскости до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. Различают вертикальные (а), горизонтальные (б) и наклонные (в) асимптоты.

2

а) б)

в)

Вертикальные асимптоты функции следует искать либо в точках разрыва второго рода (хотя бы один из односторонних пределов функции равен в точке бесконечности или не существует), либо на концах ее области определения (a,b), если a,b –конечные числа.

Если функция определена на всей числовой оси и существует конечный предел , либо , то прямая, задаваемая уравнением , является правосторонней горизонтальной асимптотой, а прямая - левосторонней горизонтальной асимптотой.

Если существуют конечные пределы