Учебное пособие: Исследование функций и построение их графиков

Сократим дробь на множитель и вычислим ее при

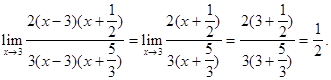
Пример 4.

Решение. Непосредственной подстановкой убеждаемся, что возникает неопределенность вида . Для раскрытия неопределенности умножим числитель и знаменатель на выражение , являющееся сопряженным к знаменателю

= .

Пример 5. .

Решение. Имеем неопределенность вида . Разделим числитель и знаменатель на (в более общем случае, когда числитель и знаменатель представляют многочлены разных степеней, делят на с наибольшим показателем степени числителя и знаменателя). Используя свойства пределов, получим:

.

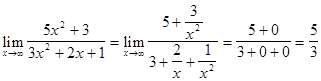Пример 6. .

Решение. При имеем неопределенность вида . Представим , разделим и умножим числитель и знаменатель на числа 2, 5 и , тогда предел преобразуется к виду:

.

Пользуясь свойствами пределов и первым замечательным пределом, далее имеем:

.

Пример 7. .

Решение. Имеем неопределенность вида [], так как

, а .

Выделим у дроби целую часть

.

Введем новую переменную и выразим отсюда через : . Тогда

Заметим, что при переменная . Теперь, переходя к новой переменной и используя второй замечательный предел, получим:

=.

Неопределенности вида путем алгебраических преобразований приводятся к виду . Неопределенности вида , можно раскрыть, предварительно прологарифмировав соответствующую функцию. Неопределенности вида можно исключить, используя правило Лопиталя, которое изложено в конце темы 2.

Пример 8. Первоначальный вклад в банк составил денежных единиц. Банк выплачивает ежегодно % годовых. Необходимо найти размер вклада через лет при непрерывном начислении процентов. Решить задачу при =10, =5%, =20 лет.

Решение. При % годовых размер вклада ежегодно будет увеличиваться в

раз, т.е. .

Если начислять проценты по вкладам не один раз в год, а раз, то размер вклада за лет при начислениях составит