Учебное пособие: Исследование функций и построение их графиков
Вопросы для самопроверки
Дайте определение производной функции в точке.
Какая функция называется дифференцируемой в точке?
Назовите важнейшие правила дифференцирования.
Как находится производная сложной функции?
Сформулируйте правило Лопиталя.
Задачи для самостоятельной работы
Найти производные следующих функций:
Таблица 3.
| Номер варианта | А) | Б) | В) |
| 1 | y=(3x4-4x(-1/4)+2)5 | y=arccos2x+(1-4x2)1/2 | y=2tgx+x sin(2x |
| 2 | y=(5x2+4x(5/4)+3)3 | y=arctg(x2-1)1/2 | y=e3x-2x tg(3x) |
| 3 | y=(0.25x8+8x(3/8)-1)3 | y=arccos(1-x2)1/2 | y=3cosx-x sin(2x) |
| 4 | y=(0.2x5-3x(4/3)-4)4 | y=arctg(x-1)1/2 |  |
| 5 | y=(3x8+5x(2/5)-3)5 | y=arctg(2/(x-3)) |  |
| 6 | y=(5x4-2x(-3/2)+3)4 | y=arccos(1-x)1/2 |  |
| 7 | y=(4x3+3x(-4/3)-2)5 | y=arcctg(x-1)1/2 |  |
| 8 | y=(7x5-3x(5/3)-6)4 | y=arcsin3x-(1-9x2)1/2 | y=etgx-x1/2 cos(2x). |
| 9 | y=(3x4-4x(-1/4)-3)5 | y=arctg(1/(x-1)) | y=x tg3x+2x-2 |
| 10 | y=(8x3-9x(-7/3)+6)5 | y=arcsin((1-x)1/2) |  |
Тема 3. Применение дифференциала функции в приближенных вычислениях
Дифференциалом функции 
в точке 
называется главная, линейная относительно приращения аргумента 
часть приращения функции 
, равная произведению производной функции в точке на приращение независимой переменной:
.
Отсюда приращение функции отличается от ее дифференциала 
на бесконечно малую величину и при достаточно малых значениях можно считать 
или
.
Приведенная формула используется в приближенных вычислениях.
Пример. Вычислить приближенно 
Решение. Рассмотрим функцию 
. Это степенная функция и ее производная найдется:
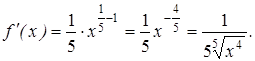
В качестве требуется взять число, удовлетворяющее условиям:
- значение 
известно или достаточно просто вычисляется;
- число должно быть близким к числу 33,2, т.е. приращение 
должно быть как можно меньше.
В нашем случае этим требованиям удовлетворяет число = 32, для которого 
= 2, = 33,2 -32 = 1,2.
Применяя формулу, находим искомое число:
+ 
.
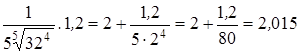Вопросы для самопроверки
1. Дайте определение дифференциала функции в точке.
2. Почему формула, используемая для вычислений, является приближенной?
3. Каким условиям должно удовлетворять число 
, входящее в приведенную формулу?