Учебное пособие: Математична обробка результатів вимірів

де , так як поява однієї із можливих подій є достовірна подія.

Якщо випадкова величина X має нескінченне число можливих значень, то

Математичним сподіванням випадкової величини X називається сума добутку всіх можливих значень випадкової величини на ймовірності цих значень.

Математичним сподіванням неперервної випадкової величини X, можливі значення якої належать відрізку [а, в], називають визначений інтеграл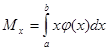

а де (х) - щільність імовірності розподілу випадкової величини.

Математичне сподівання має ту ж розмірність, що і випадкова величина, та має властивості:

1. Математичне сподівання постійної величини дорівнює величині постійної, тобто М(С) = С.

2. Постійний множник можна виносити за знак математичного сподівання М(СХ) = СМ_Х .

3. Математичне сподівання суми декількох випадкових величин дорівнює сумі їх математичних сподівань M (x+y+…+k) = M_x + M_y + … + M_k

4. Математичне сподівання добутку декількох взаємно незалежних випадкових величин дорівнює добутку їх математичних сподівань

Математичне сподівання може бути як додатнім, так і від'ємним.

Відомо, що для повної групи подій .

Таким чином, виявляється механічна інтерпретація математичного сподівання. Воно буде абсцисою центру тяжіння системи матеріальних точок.

Якщо ймовірності появи випадкових величин x_і тобто

де X - середнє арифметичне значення випадкової величини.

Це означає, що математичне сподівання приблизно дорівнює середньому арифметичному значенню випадкової величини. Воно буде тим точніше, чим більше буде проведено дослідів.

2) Мода і медіана випадкової величини

Модою Мо дискретної випадкової величини називають таке її значення, що має найбільшу ймовірність.

Практично, якщо маємо дискретний ряд розподілу, то знаходимо таке k-е значення випадкової величини х, що має найбільшу величину ймовірності P_n (k).

Для неперервної випадкової величини модою буде таке її значення, що має максимум щільності розподілу, тобто (Мо) = mах.

Якщо многокутник розподілу або крива розподілу має два або більше максимумів, то такий розподіл називають двохмодальним чи багатомодальним.

Медіаною Ме випадкової величини X називають таке її значення, відносно якого ймовірність появи як більшого, так і меншого значення випадкової величини X має приблизно однакову ймовірність, тобто

Геометрична медіана - це абсциса точки, де площа кривої розподілу розділяється наполовину. Тоді функція розподілу в точці Ме дорівнює математичне сподівання, мода і медіана збігаються, тобто

3) Дисперсія і середнє квадратичне відхилення