Учебное пособие: Математична обробка результатів вимірів

Величину називають центрованою випадковою величиною. Так як імовірність появи центрованих випадкових величин X справа і зліва від Мх однакова, то її математичне сподівання дорівнює нулю і не може характеризувати розсіювання її значень. Тому якістю міри розсіювання X беруть математичне сподівання від квадрата відхилення випадкової величини від її математичного сподівання і називають його дисперсією.

Дисперсією випадкової величини є математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання, тобто

Для дискретної випадкової величини дисперсія матиме вигляд суми

для неперервної це буде інтеграл

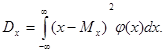
Дисперсія має розмірність квадрата розмірності випадкової величини, що не зовсім зручно. Тому для характеристики міри розсіювання випадкової величини приймають додатковий квадратичний корінь із дисперсії. Цю характеристику називають середнім квадратичним відхиленням або стандартам і позначають символом

Стандарт має таку саму розмірність, як і випадкова величина X. Дисперсія має такі властивості:

1. Дисперсія постійної величини дорівнює нулю D (C) = 0.

2. Дисперсія добутку постійної величини на випадкову величину дорівнює добутку квадрата постійної величини на дисперсію випадкової величини D(CX) = C² D_x

Якщо маємо декілька таких добутків, то

3. Дисперсія випадкової величини дорівнює математичному сподіванню її квадрата мінус квадрат її математичного сподівання

4). Моменти випадкової величини

Узагальненням основних числових характеристик випадкових величин є моменти випадкової вел