dy = f ¢ ( x ) dx .

Некоторые свойства неопределенного и определенного интегралов:

Н.и. , где с – некоторое число,

О.и.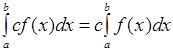, где с – некоторое число;

Н.и.,

О.и. .

!!! Неопределенный интеграл находится приведением интеграла к табличному (сумме табличных) с помощью этих двух свойств или с помощью таких приемов, как методы интегрирования заменой переменных и по частям.

Формула замены переменной в неопределенном интеграле:

, где - функция, дифференцируемая на рассматриваемом промежутке.

Формула замены переменной в определенном интеграле:

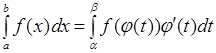, где - функция имеет непрерывную производную на отрезке [ a , b ].

Формула интегрирования по частям в неопределенном интеграле:

,

где u = u ( x ), v = v ( x ) – дифференцируемые функции переменной х.

При этом

Постоянную С в выражении для v в формуле интегрирования по частям полагают равной 0.

Формула интегрирования по частям в определенном интеграле:

,

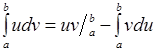где u = u ( x ), v = v ( x ) – функции, имеющие непрерывные производные на отрезке [ a , b ].

Табличные интегралы

;

;

;

;

;

;

;

;

;

.
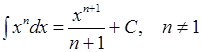
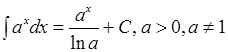
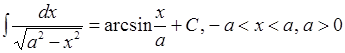
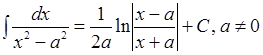
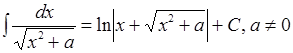