6. Если .

Виды неопределенностей

.

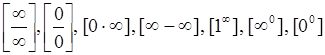!!! Основной задачей при вычислении пределов является устранение неопределенностей с помощью алгебраических преобразований.

1) для неопределенности вида :

- Если в числителе и знаменателе сложные степенные или показательные функции и . Вычисление пределов в случае отношения степенных функций производится путем вынесения за скобку в числителе и знаменателе дроби переменной x в наибольшей степени среди всех слагаемых дроби (неопределенность устраняется после сокращения дроби и применения основных теорем о пределах); в случае показательных функций за скобку выносится наибольшее слагаемое.

- Правило Лопиталя: Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле, т.е.

.

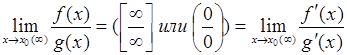2) для неопределенности вида :

- Если возможно, то числитель и знаменатель разложить на множители. Неопределенность устраняется после сокращения дроби.

- Числитель и знаменатель дроби домножить на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.

Формулы сокращенного умножения:

(a-b)(a+b)= a² -b²

(a-b)(a² +ab+b² )=a³ -b³

- Правило Лопиталя.

3) для неопределенности вида [0]:

- Выражение, представляющее собой произведение функций, нужно преобразовать в частное (не меняя смысла). После чего неопределенность преобразуется к виду или .

4) для неопределенности вида []:

- Если функция, стоящая под знаком предела, представляет собой сумму или разность дробей, то неопределенность или устраняется, или приводится к типу после приведения к общему знаменателю.

- Если функция, стоящая под знаком предела, представляет собой разность или сумму иррациональных выражений, то неопределенность или устраняется, или приводится к типу путем домножения и деления функции на одно и то же выражение, приводящее к формулам сокращенного умножения.

5) для неопределенности вида []:

- Выражение, стоящее под знаком предела представляет собой степенно-показательную функцию (в основании которой необходимо выделить целую часть дроби). Неопределенность устраняется при помощи выделения второго замечательного предела.

Формула второго замечательного предела:

; .

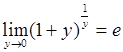ПРОИЗВОДНАЯ

Определение: Производной функции y = f ( x ) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к 0 (если этот предел существует):

Если функции u ( x ) и v ( x ) дифференцируемые, то справедливы следующие правила дифференцирования :

(u+v) ¢ =u ¢ +v ¢

(u-v) ¢ =u ¢ -v ¢

(uv) ¢ =u ¢ v+uv ¢