Учебное пособие: Моделирование электрических цепей в системе Mathcad
При А =-А Т – матрица кососимметричная.
1.2 Арифметические операции над матрицами
1.2.1 Сложение
Сумма матриц А и В
С = А + В (1.6)
получается сложением каждого элемента матриц А и В одного размера m ´n , т.е. ![]() для всех i и j .
для всех i и j .
Операция сложения матриц коммутативна
А + В = В + А (1.7)
и ассоциативна
А + (В + С) = (А + В) + С, (1.8)
а также
(А + В)Т = АТ + ВТ . (1.9)
1.2.2 Умножение матриц
Произведение С = А × В может быть получено тогда и только тогда, когда число столбцов матрицы А равно числу строк матрицы В .
Если А размера m ´t и В размера t ´n , то матрица С = А × В определяется формулой
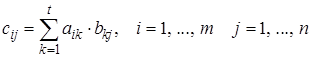 . (1.10)
. (1.10)
Заметим, что в общем случае А × В ≠ В × А .
Если А × В=В × А , то матрицы коммутирующие или перестановочные.
Умножение обладает свойствами:
А × (В × С) = (А × В) × С (1.11)
ассоциативности и
(А+В) × С=А × С+В × С и А × (В+С)=А × В+А × С (1.12)
дистрибутивности.
1.2.3 Умножение на скаляр
Умножение матрицы (А) на скаляр b означает, что каждый элемент матрицы умножается на скаляр
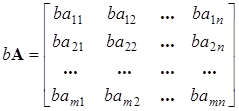 (1.13)
(1.13)
1.2.4. Вычисление определителей
Пусть А – квадратная матрица порядка n , n > 1:
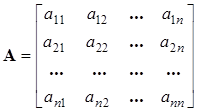 .
.