Учебное пособие: Моделирование электрических цепей в системе Mathcad

Введение

Большинство проблем, связанных с анализом схем электрических цепей, решается в два этапа. Первый этап заключается в составлении уравнений электрической цепи в форме, позволяющей использовать законы Кирхгофа и характеристики элементов, входящих в схему. Полученные на этом этапе уравнения представляют математическую модель цепи. Второй этап заключается в решении этих уравнений путем подходящих аналитических или численных методов. При машинном анализе электрических схем оба этапа могут выполняться ЭВМ, а программу общего анализа часто называют машинной моделью.

В настоящее время имеется достаточно много пакетов программ (PSpice, ElectronicWorkbench, P-Cad) для решения электрических (электронных) схем.

Любая такая программа машинного анализа схем признает и допускает лишь базовый на6ор схемных элементов, для которых она была разработана.

Чем больший базовый набор допускает программа, тем более многофункциональной она становится.

В случае, если схема содержит элементы, не входящие в базовый набор, следует заменить каждый такой элемент некоторой «эквивалентной схемой» на основе базовых элементов. Это часто невозможно, однако, в большинстве практических случаев считается возможным заменить каждый не допускаемый элемент «почти эквивалентной схемой», называемой схемной моделью. При разработке схемной модели необходимо, чтобы она имела такое же количество полюсов, что и рассматриваемый элемент, состояла лишь из элементов, входящих в базовый набор, чтобы результирующая схема аппроксимировала характеристики соответствующего элемента с переменной точностью.

Выбор наиболее подходящей модели зависит от ее правильного соответствия режима работы цепи: динамическому переходному режиму, установившемуся синусоидальному режиму или режиму постоянного тока.

Для синтеза нелинейных моделей по переменному току возможны два подхода, которые качественно согласуются с режимом работы реальных элементов: это физический метод и метод «черного ящика».

В физическом методе делается попытка преобразовать физическую структуру и механизм работы данного прибора (элемента) в схемную модель.

В методе «черного ящика» полная характеристика схемной модели и моделируемого элемента, полученная экспериментально, должны совпадать с заданной степенью точности. При этом сначала строится статическая модель, а затем для построения модели по переменному току к ней добавляются паразитные ёмкости и индуктивности в существенно важных местах и нет необходимости понимать внутренний физический механизм работы прибора.

Успешное моделирование элементов цепи и создание их схемных моделей позволяет разработать электрическую схему, состоящую только из базовых элементов, которая используется при формировании математической модели (системы уравнений, адекватно описывающей процессы рассматриваемой цепи).

Использование пакета MathCAD в практикуме по решению задач электрических цепей позволяет при освоении курса разделить этапы формирования уравнений и численного их решения, избавляя от рутинных вычислений.

Самостоятельное формирование (моделирование) уравнений, основанных на топологии, способствует их успешному освоению, а возможность изменения численных методов их решения – подходящему их выбору.

Такой подход может быть плодотворным при освоении методов анализа электрических цепей и разработке новых.

1. Элементы теории матриц

1.1 Определение матрицы

Матрица – это прямоугольная таблица чисел. Элемент с номерами ij матрицы А, а _ij находится на пересечении i -й строки и j -го столбца:

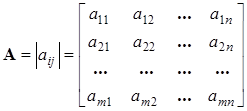. (1.1)

Матрица размера (m ´n ) (или m ´n – матрица) имеет m строк и n столбцов. У квадратной матрицы m = n . Если а ij =0 при i ≠ j , то квадратная матрица диагональная. Если в диагональной матрице все диагональные элементы равны 1, матрица называется единичной:

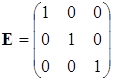. (1.2)

Если у квадратной матрицы расположенные выше (ниже) главной диагонали элементы равны нулю, то матрица – нижне – (верхне-) треугольная:

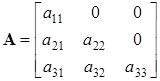. (1.3)

Если у матрицы лишь один столбец или строка, в этом случае она называется столбцовой или строчной, или вектор-столбец, или вектор-строка, или просто вектор.

Вектор-столбец:

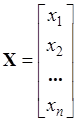. (1.4)

Вектор-строка:

. (1.5)

Матрица А ^Т называется транспонированной к А , если элемент а _ij матрицы А равен элементу а _ji матрицы А ^Т для всех i и j

Пример 1.1. Если .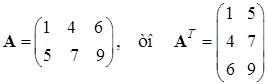

--> ЧИТАТЬ ПОЛНОСТЬЮ <--