Учебное пособие: Моделирование электрических цепей в системе Mathcad
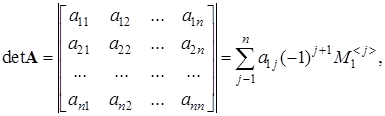
где ![]() – определитель квадратной матрицы порядка n -1, полученной из матрицы А вычеркиванием первой строки и j -того столбца.
– определитель квадратной матрицы порядка n -1, полученной из матрицы А вычеркиванием первой строки и j -того столбца.
Формулу 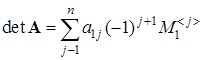 называют формулой вычисления определителя разложением по первой строке . Число
называют формулой вычисления определителя разложением по первой строке . Число ![]() называется алгебраическим дополнением элемента a 1 j .
называется алгебраическим дополнением элемента a 1 j .
1.2.5 Обращение матрицы
Если А и В- две квадратные матрицы порядка n , такие, что
А × В=Е, (1.14)
то говорят, что В -матрица, обратная к А, и обозначается через
В=А -1 ,(1.15)
заметим, что А × А- 1 =А- 1 × А=Е,
![]() (1.16)
(1.16)
где D =detА (определитель матрицы А ); ![]() – алгебраическое дополнение элемента а ij . , а Мij минор к элементу aij (определитель, полученный из А удалением i-й строки и j-ого столбца.
– алгебраическое дополнение элемента а ij . , а Мij минор к элементу aij (определитель, полученный из А удалением i-й строки и j-ого столбца.
Обращение обладает свойствами:
![]() (1.17)
(1.17)
А -1 существует, если detA ¹0.
Если detA =0, то матрица особенная.
1.3 Матричное представление линейных уравнений
Система линейных уравнений может быть записана в виде матричного уравнения:
А × Х=В . (1.18)
Ее решение получаем, умножая обе части равенства слева на А -1 :
А -1 ×А × Х =1×Х =А -1 ×В ,
то есть:
Х =А -1 ×В . (1.19)
Это удобный способ выразить решение Х , но существуют методы решения значительно лучше, чем явное формирование матрицы А -1 и умножение ее на В .
1.4 Используемые инструменты MathCAD
Большинство вычислений с матрицами, как и другие вычисления в Mathcad, можно выполнить тремя способами: с помощью панелей инструментов, выбором операции в меню или обращением к соответствующей функции.
Панель операций с матрицами и векторами в Matrix открывается щелчком по кнопке ![]() в панели математических инструментов. За кнопками панели закреплены следующие функции:
в панели математических инструментов. За кнопками панели закреплены следующие функции:
![]() – определение размеров матрицы;
– определение размеров матрицы;
![]() – ввод нижнего индекса;
– ввод нижнего индекса;
![]() – вычисление обратной матрицы;
– вычисление обратной матрицы;
![]() – вычисление определителя матрицы:
– вычисление определителя матрицы: ![]() ;
;