Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго и первого порядков
 =0,
=0,
![]() .
.
Характеристическими числами для точки О (0,0), будут ![]()
![]()
Так как один корень нулевой, тогда точка О (0,0) является сложным состоянием равновесия (изолированное состояние равновесия), для которого требуется дополнительное исследование. Для определения характера состояния равновесия О (0,0) воспользуемся теоремой [5].
Теорема 2.1 Пусть точка (0,0) – изолированное состояние равновесия системы:
![]()

где φ ( x , y ), ψ ( x , y ) – полиномы от x , y начиная со второй степени, y =φ( x ) – решение уравнения y + Q 2 ( x , y )=0, а разложение функции ψ( x )= P 2 ( x , φ( x )) имеет вид:
![]()
Тогда:
1) при m -нечётном и ∆ m >0 точка (0,0) – есть топологический узел;
2) при m -нечётном и ∆ m <0 точка (0,0) – есть топологическое седло;
3) при m -чётном точка (0,0) есть седло-узел, то есть такое состояние равновесия, каноническая окрестность которого состоит из параболического и двух гиперболических секторов; При этом:
а) если ∆ m <0, то внутри гиперболических
секторов заключён отрезок положительной
полуоси ОХ, примыкающий к точке (0,0);
б) если ∆ m <0, то – отрезок отрицательной
полуоси ОХ.
Чтобы воспользоваться теоремой, необходимо систему (2.7) привести к виду:
 (2.10)
(2.10)
Это возможно сделать, воспользовавшись одним из следующих преобразований:
1. если в≠0 , 
2. если в =0, а =0, 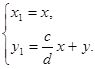
3. если в =0, d =0, 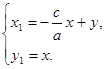
где а, в, с, d – коэффициенты системы (2.7).
Для системы (2.7) воспользуемся следующим преобразованием:

Получим: