Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго и первого порядков

Характеристическими числами для точки А() системы (2.7) будут λ₁ =–4d, λ₂ =d.

Корни λ₁ , λ₂ –действительные и одного знака, зависящие от параметра d. Если d<0, тогда точка А() – неустойчивый узел; если d>0, тогда точка А() – устойчивый узел.

Исследуем бесконечно-удалённую часть плоскости системы (2.7) вне концов оси ОУ. Преобразование [1] переводит систему (2.7) в систему:

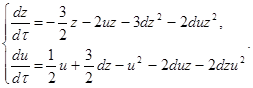(2.12)

где t=zτ, dt=zdτ.

Изучим бесконечно-удалённые точки на оси U, то есть z=0. Получаем:

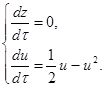
Следовательно, u ₁ =0, u ₂ = .

Таким образом, получили две точки N₁ (0,0), N₂ (0,), которые являются состояниями равновесия. Исследуем характер этих точек обычным способом.

1. Исследуем точку N₁ (0,0).

Составим характеристическое уравнение в точке N₁ (0,0):

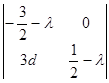=0,

λ₁ = , λ₂ =.

Корни λ₁ ,λ₂ –действительные и различных знаков, следовательно, точка N₁ (0,0) – седло.

2. Исследуем точку N₂ (0,).

Составим характеристическое уравнение в точке N₂ (0,):

P_z = –2u-6dz-4duz,

P_u =–2z-2dz² ,

Q_z = d-2du-2du² ,

Q_u = –2u-2dz-4duz.

Характеристическое уравнение имеет вид:

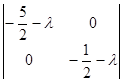=0.

Следовательно, характеристические числа:

λ₁ =, λ₂ =.

Корни λ₁ ,λ₂ –действительные, различных знаков, значит точка N₂ (0,) является седлом.

Исследуем бесконечно-удалённые концы оси ОУ с помощью преобразования [1] x=, y=.Это преобразование переводит (2.7) в систему:

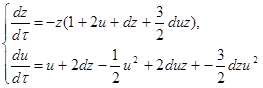
где t=zτ, dt=zdτ.

Для исследования состояний равновесия на концах оси ОУ, нам необходимо исследовать только точку (0,0), которая является состоянием равновесия данной системы. Составим характеристическое уравнение в точке (0,0):