Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго и первого порядков

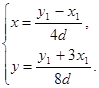
Следовательно, можем найти:

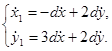
Тогда:

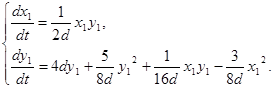
Чтобы данную систему привести к системе вида (2.10), сделаем замену тогда dt =dh и получим систему:

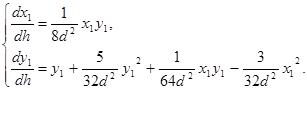
Найдём решение уравнения:

y₁ + (2.11)

в виде ряда по степеням y ₁ :

y ₁ = φ ( x ₁ )= c ₁ x ₁ + c ₂ x ₁ ² +….

Подставим y ₁ = c ₁ x ₁ + c ₂ x ₁ ² +… в уравнение (2.11), получим:

c ₁ x ₁ + c ₂ x ₁ ² + … + ( c ₁ x ₁ + c ₂ x ₁ ² +…)² + x ₁ ( c ₁ x ₁ + c ₂ x ₁ ² +…)– x ₁ ² =0.

x ₁ ¹ : с₁ =0,

x ₁ ² : с₂ +с₁ +с₁ =0,

Следовательно с₁ =0, с₂ =, ….

Тогда y₁ =φ(x₁ )= х₁ ² +….

Находим ψ(х₁ )=Р₂ (х₁ ,φ(х₁ ))=(+……)= +……..=∆_m x^m .

Получили m=3-нечётное, ∆_m >0.

Следовательно, по теореме 2.1 получаем, что точка О (0,0) – топологический узел.

2 . Исследуем точку А().

Составим характеристическое уравнение в точке А().

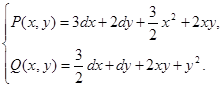
Отсюда

P_x ( x , y )=3 d +3 x +2 y ,

P_y (x, y)=2d+2x,

Q_x (x, y)=d+2y,

Q_y ( x , y )= d +2 x +2 y .

Следовательно, характеристическое уравнение имеет вид: