Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго и первого порядков
![]()
Корни λ1 ,λ2 –действительные и различных знаков, значит точка (0,0) – седло.
Теперь дадим распределение состояний равновесия системы (2.7) в виде таблицы 2.
Таблица 2
| d | O (0,0) | A( | ∞ | ||
| N0 | N1 | N2 | |||
| (-∞; 0) |
Топологическое Узел |
Неустойчивый Узел | Седло |
Устойчивый Узел |
Седло |
| (0;∞) |
Топологическое Узел |
Устойчивый Узел | Седло |
Устойчивый Узел | Седло |
Положение кривых (2.8), (2.9) и расположение относительно их состояний равновесия при d<0 и d>0 даётся соответственно рис. 2 (а, б).
Поведение траекторий системы (2.7) в целом при d<0, d>0 представлено на рис. 4 (а, б) приложения Б.
Так как Воробьёв А.П. [10] доказал, что для систем, правые части которых есть полиномы второй степени, предельный цикл может окружать только точку типа фокуса, тогда исследуя вид кривых (2.8), (2.9) и расположение относительно их состояний равновесия, убеждаемся, что система (2.7) не имеет предельных циклов.
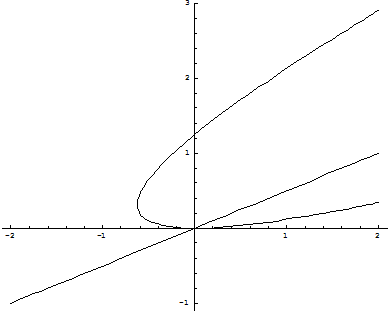
a) d<0
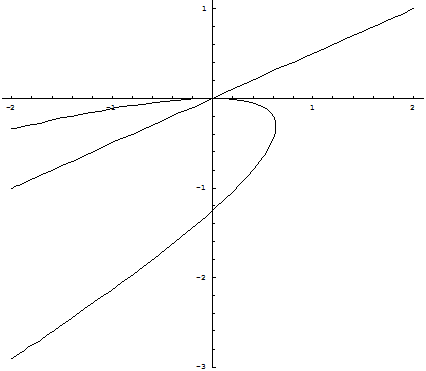
б) d>0
Рис. 2
Заключение