Исходные данные:

Вариант №	y0	y1	y2	y3	y4	y5	h	x0
64	-0.02	0.604	0.292	-0.512	-1.284	-2.04	0.5	0.3

Задача 1

Исходные данные вводятся в ЭВМ как абсолютно точные числа и представляются в ней в виде чисел с плавающей точкой с относительной погрешностью в одну миллионную. Введенные данные x₀ и y₀ служат основой формирования двух векторов x=(x₀ , x₁ , …, x_n ) и y=(y₀ , y₁ , …, y_n ) по рекуррентным формулам:

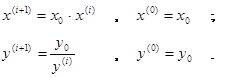Вычислить скалярное произведение с := ( x , y ) по алгоритму:

с := 0; i := 0;

while i < n + 1 do c := c + x_i · y_i ;

и оценить аналитически и численно инструментальную абсолютную и относительную погрешности.

Решение

Поскольку данные представляются в ЭВМ в виде чисел с плавающей точкой с относительной погрешностью, то

x₀ = x₀ (1+δ)

y₀ = y₀ (1+δ)

C₀ = x₀ y₀ (1+δ)

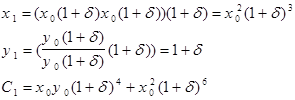???i = 1

Приi = 2

x₂ = x₀ ³ (1+δ)⁵

y₂ = y₀ (1+δ)³

C₂ = x₀ y₀ (1+δ)⁵ + x₀ ² (1+δ)⁷ + x₀ ³ y₀ (1+δ)¹⁰

Приi = 3

x₃ = x₀ ⁴ (1+δ)⁷

y₃ = (1+δ)⁵

C₃ = x₀ y₀ (1+δ)⁶ + x₀ ² (1+δ)⁸ + x₀ ³ y₀ (1+δ)¹¹ + x₀ ⁴ (1+δ)¹⁴

При i = 4

x₄ = x₀ ⁵ (1+δ)⁹

y₄ = y₀ (1+δ)⁷

C₄ = x₀ y₀ (1+δ)⁷ + x₀ ² (1+δ)⁹ + x₀ ³ y₀ (1+δ)¹² + x₀ ⁴ (1+δ)¹⁵ + x₀ ⁵ y₀ (1+δ)¹⁸

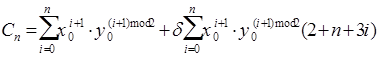Выявим закономерность изменения C_i :

При расчете C_n без учета погрешности исходных данных и погрешности вычисления, получим

Обозначим эту сумму как S₁ .

Тогда абсолютная погрешность S₂

а относительная погрешность

Оценим инструментально относительную и абсолютные погрешности при n = 10

--> ЧИТАТЬ ПОЛНОСТЬЮ <--