Решение.

Из задачи 14 возьмем полином Чебышева T₄ = 8x⁴ - 8x² + 1. В качестве начального приближения к корню возьмем x_нач , вычисленное по формуле

Т.к. 8x⁴ - 8x² + 1 = 0, то можем сказать, что f(x_нач + α) = 0

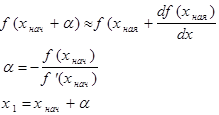Воспользуемся DERIVE для нахождения корня с необходимой точностью:

получим такие значения: 0.38234, 0.382689, 0.382683, 0.382683, 0.382683.

На третьей итерации получаются значения корня с нужной точностью.

Задача 19

Скорость изменения переменной x(t) во времени равна функции от этой переменной f(x). Найти аналитическое выражение последней от времени, начиная с t = 0, если в начальный момент x(0) = 0. В качестве f(x) взять степенной многочлен P₂ (x), полученный в задаче 8. Протабулировать полученное решение с шагом h = 0.1 в интервале [0, 0.5].

Решение

P₂ (x) = -0.0710314 + 0.989486x – 0.624589x²
= f(x)

Исходя из начальных условий, т.к. dx/dt = f(x), имеем

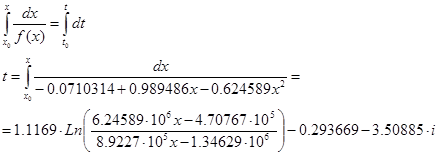
Т.к. x = F(t), то:

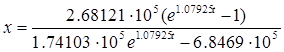
Протабулируем x(t) на интервале [0; 0.5] c шагом h = 0.1:

t = 0 x = 0

t = 0.1 x = -0.0622648

t = 0.2 x = -0.137833

t = 0.3 x = -0.230872

t = 0.4 x = -0.347464

t = 0.5 x = -0.496850

Задача 20

Методом Эйлера в интервале [0, 0.5] с шагом h = 0.1 получить решение нелинейного дифференциального уравнения:

dx/dt = a + bx + cx² ,

x(0) = 0

Коэффициенты a, b, c взять из P₂ (x), полученного в задаче 8.

Решение

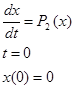y = P₂ (x)

P₂ (x) = -0.0710314 + 0.989486x – 0.624589x²

Общая формула для решения