Контрольная работа: Математический анализ
x1 = 0 + 0.5· (-0.0710314) = -0.0355156
x2 = -0.0355156 + 0.5·(-0.0710314 + 0.989486 (-0.0355156)1 –
-0.624589· (-0.03551562 ) = -0.053854
x3 = -0.053854 + 0.5· (-0.0710314 + 0.989486 (-0.053854)1 –
- 0.624589 (-0.053854)2 ) = -0.0636315
x4 = -0.0636315 + 0.5· (-0.0710314 + 0.989486 (-0.0636315)1 –
-0.624589 (-0.0636315)2 ) = -0.0689304
x5 = -0.0689304 + 0.5 (-0.0710314 + 0.989486 (-0.0689304)1 –
-0. 0.624589 (-0.0689304)2 ) =--0.071827
Задача 23
Проверить заданную систему из трех векторов на линейную зависимость. При обнаружении линейной зависимости поменять местами первые компоненты векторов x1,x2 и выполнить повторную проверку. Из исходных данных векторы формируются так:
x1 = (y0 ,y1 ,y2 ); x2 =(y3 ,y4 ,y5 ); x3 =(h,x0 ,0).
На базе линейно независимой системы векторов x1 , x2 , x3 методом Грама-Шмидта построить ортонормированную систему трех векторов:
y1 = (y11 ,y21 ,y31 ); y2 =(y12 ,y22 ,y32 ); y3 =(y13 ,y23 ,y33 ).
На основе полученной системы векторов сформировать квадратную матрицу T = (y1 ,y2 , y3 ). Вычислить det(T) и получить матрицы — обратную T-1 и транспонированную T’. Найти произведение T-1 · T, T · T’. Сделать выводы о свойствах матрицы T.
Решение
Исходные векторы x1 = (-0.02,0.604,0.292); x2 =(-0.512,-1.284,-2.04);
x3 =(0.5,0.3,0).
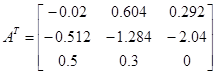
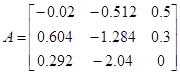
Составим матрицу и проверим ее на линейную зависимость:
det (A·AT ) = 0.23591 > 0, значит система линейно независима.
Найдем векторы v1 , v2 , v3
![]() v1 = x1
v1 = x1
v2 = x2 + a21 ·v1
v3 = x3 + a32 ·v2 + a31 ·v1
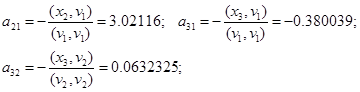
v1 = (-0.02, 0.604, 0.292);
v2 = (-0.572423, 0.54078, -1.15782);
v3 = (0.471405, 0.104651, -0.184183).