Контрольная работа: Математический анализ

Матрица T:

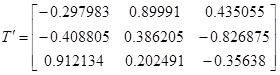
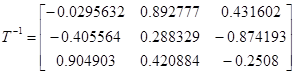
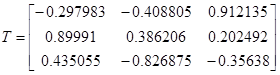
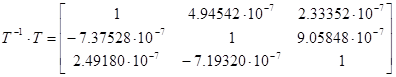det(T) = -1

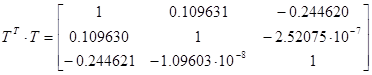Ортонормированная матрица T состоит из собственных векторов. Определитель матрицы T равен 1. Если транспонировать ортогональную матрицу то она будет равна обратной. T’ = T^-1 . Это значит, что если умножить T·T’ = E — получим единичную матрицу.

Задача 24

Считая числа –1, -2, -3 собственными значениями, а векторы у₁ , у₂ , у₃ из задачи 23 – собственными векторами некоторой матрицы А, найдите проекторы этой матрицы ( Р₁ , Р₂ , Р₃ ), саму матрицу А и ей обратную А_-1 . Получить характеристическое уравнение матрицы А и подтвердить правильность всех промежуточных вычислений.

Решение

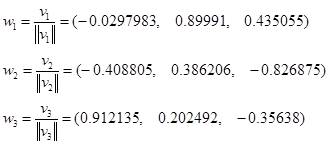
Найдем проекторы матрицы А:

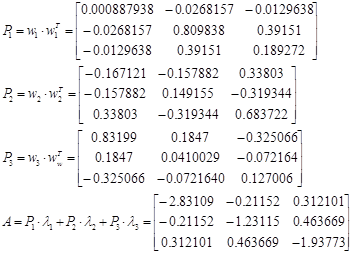
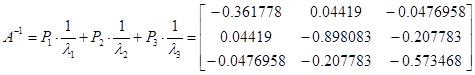
Найдем обратную матрицу А^-1 :

Характеристическое уравнение матрицы А имеет вид:

-x³ -6x² -11x-6=0;

Корни характеристического уравнения – собственные значения матрицы

x₁ = -1; x₂ = -2; x₃ = -3

Задача 25

Решить систему алгебраических уравнений А·x = b, где А- матрица коэффициентов из задачи 24, x = (x1, x2, x3) – векторы решения, b = (3, 2, 1) – вектор правых частей. Решение получить, используя обратную матрицу, полученную из задачи 24.

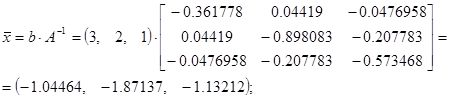Решение