Контрольная работа: Математический анализ

Оценить погрешность определенного интеграла от функции sin(x) в пределах [0,2/3π] по квадратурной формуле наивысшей алгебраической степени точности, полученной в задаче № 10в, по сравнению с аналитически точным. Проделать то же самое над усеченным степенным рядом, представляющим sin(x), в который x входит со степенью не выше третьей.

Решение

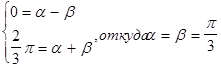???????? ?? ???????? [0,2/3 π] ? ??????? [-1,1]: ??? ????? ????????????? ???????? ??????????????? x= α + βt . ????????? ???????

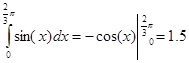
Учитывая, что dx = βdt, получим:

Применим квадратурную формулу:

Вычислим аналитически:

Найдем погрешность вычисления:

Проделаем те же операции над усеченным степенным рядом, представляющем sin(x):

Перейдем от пределов [0; 2π/3] к пределам [-1; 1], для этого используем линейное преобразование x = α +βt. Составим систему уравнений:

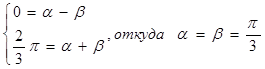
Учитывая, что dx = βdt, получим

Применим квадратурную формулу, получим

Найдем погрешность вычисления

Задача 14

Степенными полиномами Чебышева T_i относительно переменной x (|x| < 1) являются решениями линейного разностного уравнения второго порядка:

T_i+2 - 2x T_i+1 + T_i = 0,

с начальными условиями T₀ = 1 и T₁ = x.

Найти аналитическое выражение и вычислить значения полинома Чебышева i-й степени, если и i = 4. Проверить вычисления непосредственно по заданной рекуррентной формуле. Найти положение нулей и экстремумов у многочленов Чебышева в общем виде и для заданных выше x и i. Оценить модуль максимально возможного значения полинома в точках экстремумов.

Решение.

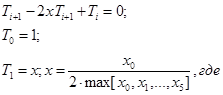
Исходя из того, что

x_i = |y_i | надо найти T₄ т.е. для i = 4

Из T_{i +2} - 2xT_{i +1} + T_i = 0 следует, что

T₂ = 2xT₁ - T₀

T₃ = 2xT₂ - T₁ = 2x(2xT₁ - T₀ ) - T₁