Контрольная работа: Математический анализ

Значение определенного интеграла найдем, исходя из формулы:

где w₁ , w₂ — некоторые коэффициенты

t₁ , t₂ ??????, ????????? ?????? ????????? ??????????????.
???????? ??????? ?????????

w(t) = (t-t₁ )(t-t₂ ) = C₀ + C₁ t + C₂ t² = 0

C₂ = 1

Домножив уравнения на соответствующие коэффициенты получим:

2C₀ + 2/3 = w₁ (C₀ + C₁ t₁ + t₁ ² ) + w₂ (C₀ + C₁ t₁ + t₂ ² )

2C₀ + 2/3 = 0

C₀ = -1/3

Подставляя полученные значения в первую систему, получим:

Квадратурная формула:

Задача 11

С помощью квадратурных формул, полученных в задаче 10, вычислить определенный интеграл от степенного представления интерполяционного многочлена Лагранжа (Ньютона), полученного в задаче № 6 в пределах от x₀ до x₀ +3h, и сравнить его с аналитически вычисленным значением определенного интеграла по первообразным многочлена.

Решение

Используем степенное представление интерполяционного многочлена Лагранжа из задачи 6

Для перехода к интегралу с канонической формой используем линейное преобразование: x = α + βt.

Составим систему уравнений:

Подставив x = 1.05 + 0.75t, получим многочлен Лагранжа от переменной t:

L (t) = 0.24975t³ - 0.80325t² - 0.49575t + 0.537253

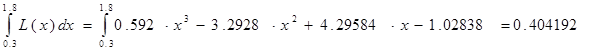Учитывая, что dx = βdt, получим:

Применим квадратурную формулу, полученную в задаче №10

??? ????????? ???????? ???????????? ???????? ?????????:

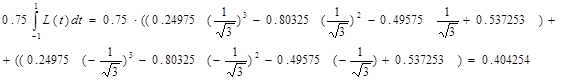Так как результаты совпали, значит, вычисления произведены верно.