Контрольная работа: Модели и методы принятия решения
3. Нахождение по всем переменным частных производных от целевой функции и функций, определяющих область допустимых решений.
4. По указанной ранее формуле (12) нахождение координаты точки, определяющей возможное новое решение.
5. Проверка, удовлетворяют ли координаты найденной точки системе ограничений задачи. Если нет, то переход к следующему этапу. Если координаты найденной точки определяют допустимое решение, то исследование необходимости перехода к последующему допустимому решению. В случае такой необходимости переход к этапу 2, в противном случае найдено приемлемое решение задачи.
6. Установка значения весовых коэффициентов и переход к этапу 4.
Построим область допустимых решений задачи (рис.5) и линии уровня, определяемые целевой функцией (11):
j (X ) = - 2x1 + 8x2 - x1 2 - x2 2
j (X ) = - (x1 2 + 2х1 + 1) + 1 - (x2 2 - 8х2 + 16) + 16
j (X ) = - (x1 + 1) 2 + 1 - (x2 - 4) 2 + 16
j (X ) = - (x1 + 1) 2 - (x2 - 4) 2 + 17 (13)
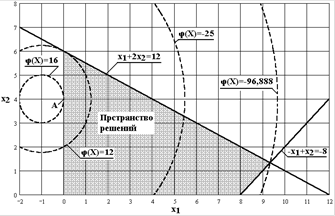
Рис.5. Область допустимых решений
Линиями уровня служат окружности с центром в точке (- 1;
4). Точка касания одной из этих окружностей с областью допустимых решений и является искомой точкой максимального значения целевой функции.
Из вида целевой функции (11) можно сделать вывод:
чем дальше точка от центра окружности, тем всё меньше целевая функция, максимум целевой функции будет в точке касания окружности вертикальной оси координат (точка А на рис.5), при этом: х1 = 0; х2 = 4
и целевая функция равна:
j (X ) = - (x1 + 1) 2 - (x2 - 4) 2 + 17 = - (0 + 1) 2 - (4 - 4) 2 + 17 = 16.
Для решения задачи методом штрафных функций примем начальное значение допустимого решения:
![]() .
.
Выбираем шаг вычислений и точность вычислений:
![]() и
и ![]() .
.
Принимаем весовые коэффициенты:
![]() ,
,
![]() .
.
Находим частные производные от целевой функции:
![]() ,
,
![]() .
.
Определяем частные производные от функций ограничения:
![]() ,
,