Контрольная работа: Модели и методы принятия решения

Ответ:

Оптимальное решение:

х₁ = 5,36

х₂ = 0,16

при этом значение целевой функции равно:

j (X ) = - 10,621.

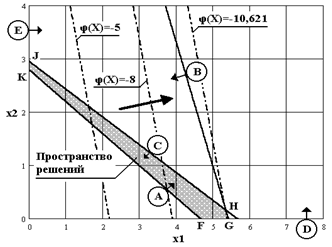
Рис.2. Нахождение оптимальной точки

Задача 2

Найти экстремумы методом множителей Лагранжа.

Решение проиллюстрировать графически.

extr j (X ) = 3x₁ ² + 2x₁ + 2x₂ ² + 4x₂ x₃

при

x₁ + 2x₂ = 19

x₁ + 2x₃ = 11.

Решение:

Обозначим:

g₁ (X ) = x₁ + 2x₂ - 19 = 0,g₂ (X ) = x₁ + 2x₃ - 11 = 0.

Функция Лагранжа имеет вид:

Отсюда получаем необходимые условия экстремума в виде системы уравнений:

,

,

,

,

.

Решаем систему уравнений через определители.

Главный определитель:

.

Матрица - столбец левой части системы (свободных членов):