Контрольная работа: Модели и методы принятия решения
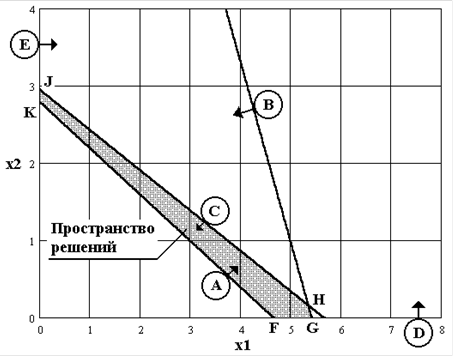
Рис.1. Нахождение оптимального решения
Ограничения:
![]() (А)
(А)
![]() (В)
(В)
![]() (С)
(С)
х2 ³ 0 (D)
х1 ³ 0 (E)
Этап 2. Нахождение оптимального решения
Точки пространства допустимых решений, показанного на рис.1, удовлетворяют одновременно всем ограничениям. Это пространство ограничено отрезками прямых, которые соединяются в угловых точках F, G, H, J и K.
Любая точка, расположенная внутри или на границе области, ограниченной ломаной FGHJK, является допустимым решением, т.к удовлетворяет всем ограничениям.
Пространство допустимых решений содержит бесконечное число точек.
Нахождение оптимального решения требует определения направления убывания целевой функции (1):
min j (X ) = - 2x1 - x2 + x3 .
Подставляем в целевую функцию найденное значение (7):
![]() .
.
Мы приравниваем j (X ) к нескольким убывающим значениям, например, (- 5) и (- 8). Эти значения, подставленные вместо j (X ) в выражение целевой функции, порождают уравнения прямых; для значений (- 5) и (- 8) получаем уравнения прямых:
![]()
и
![]() .
.
На рис.2 эти прямые показаны штрих-пунктирными линиями, а направление убывания целевой функции - толстой стрелкой.
Целевая функция может убывать до тех пор, пока прямые, соответствующие убывающим значениям этой функции, пересекают область допустимых решений. Точка пересечения области допустимых решений и прямой, соответствующей минимально возможному значению целевой функции, и будет точкой оптимума.
Из рис.2 видно, что оптимальное решение соответствует точке Н. Эта точка является местом пересечения прямых (В) и (С), поэтому её координаты х1 и х2 находятся как решение системы уравнений, задающих эти прямые:
![]()
![]()
Решением этой системы будет:
х1 = 5,36
х2 = 0,16
при этом значение целевой функции равно: